[读书笔记]《西瓜书》第九章 聚类 补充
![[读书笔记]《西瓜书》第九章 聚类 补充](/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_900x500_fit_q75_box.jpg)
第九章 聚类 补充
谱聚类(Spectral Clustering)本来这一章节的内容并没有提及这块的知识点的,相对应的内容其实是在西瓜书的第十四章节中。虽然谱聚类是源自图论中相关的知识推演出来的,但是其本身来看仍然是一种无监督的聚类算法,因此相比于在后续提到第十四章节的时候再进行补充,则更优先的补充在这个地方。
什么是谱聚类?
要想彻底的弄明白什么是谱聚类,那就一言难尽了,这块的内容我相信在网上也有不少的说明,但是为了把谱聚类知识点整理清楚,一些概念性的东西还是得整理一下,不够完整的地方在后续第十四章概率图模型中会涉及,并且在后续图神经网络中会进行补充。
首先直观的感受一下谱聚类的效果
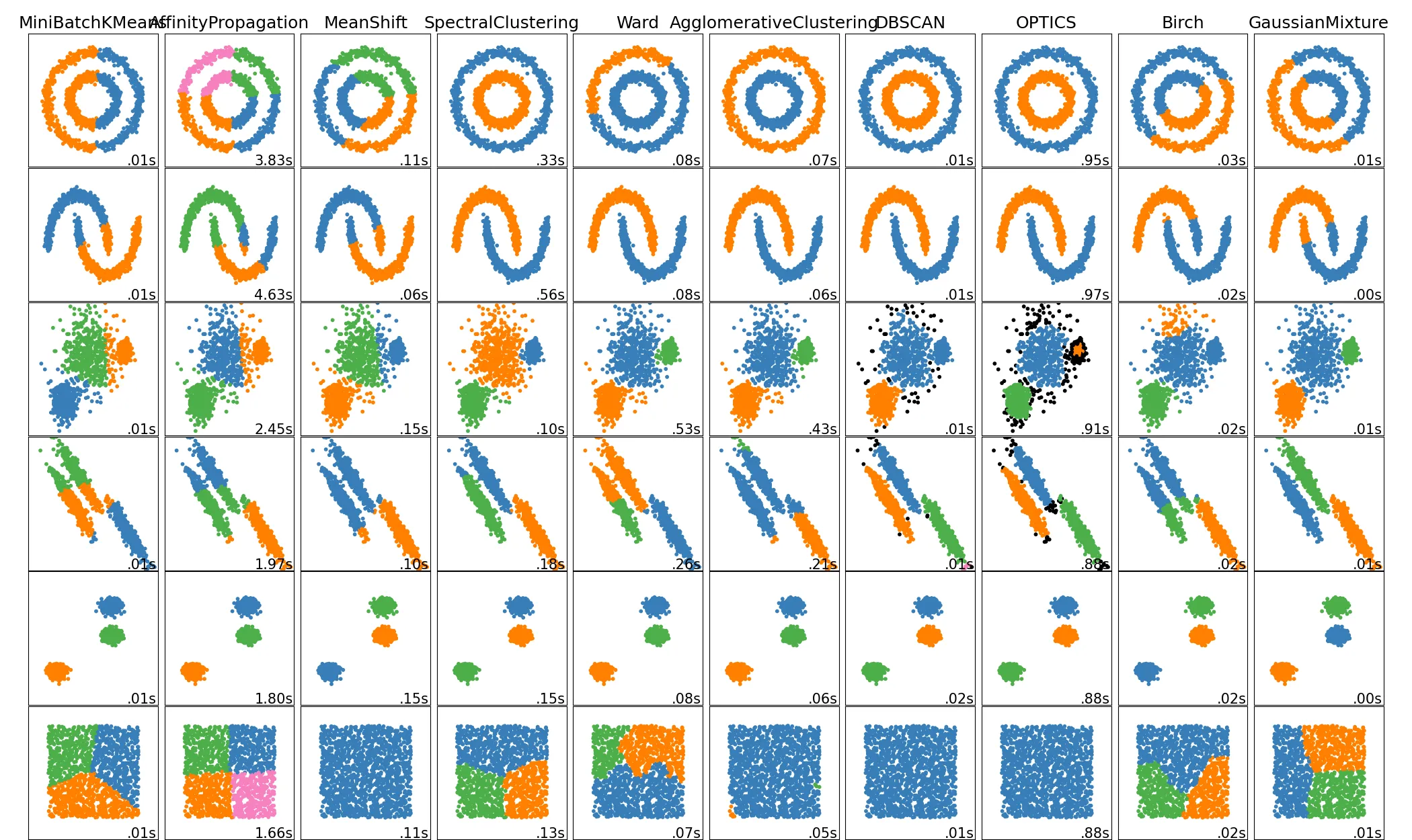
这张图片来自于scikit-learn包中关于聚类的对比Comparing different clustering algorithms on toy datasets。
从图中可以看到第四个 谱聚类(Spectral Clustering)与我们先前介绍过并学习过的 DBSCAN 聚类算法呈现的效果在前两张图片中是一致的。
PS:为什么提出这个 DBSCAN 来做类比,这一点很重要,在后面可以慢慢感受到~
整个图片看下来,我们对于 谱聚类 的聚类效果有了直观的感受,带着上面的感受我们来具体的看一看到底谱聚类在做什么?
Spatial Domain 和 Spectral Domain
PS:其实这里我自己也不是闹得很明白,本来很想在介绍谱聚类的时候把这部分的内容给绕开讲解的,但是发现没法回避,于是整理了一下我自己所理解的内容,如果不对也请见谅~
首先因为谱聚类是源自于图模型中的,因此这里就不得不介绍一下在图模型中这两个概念了。
PS:默认大家对于图模型有一定的了解了(点、边、拓扑空间、组合爆炸、NP难)等知识点~
Spatial Domain
Spatial Domain,翻译过来就是空间域,最直观的感受就是在图谱空间中节点于节点之间的所形成的的空间结构,因此在一些文献上 spatial domain 又被称做 ”vertex domain”。
Spectral Domain
Spectral Domain,翻译过来就是谱图域,有了在Spatial Domain上的定义,自然而然的就想要研究在这样形成的拓扑空间中节点的性质,于是乎引入了一种理论——谱图理论(Spectral graph theory)。
谱图理论(Spectral graph theory):主要研究的是图的拉普拉斯(Lapalacian)矩阵的特征值和所对应的特征向量对于图拓扑性质的影响,是对图空间拓扑的数学描述。
这样的解释可能还是不够直观,引用Wikipedia上关于这块的一幅图片,相信各位读者一下就能理解这两者的区别了~
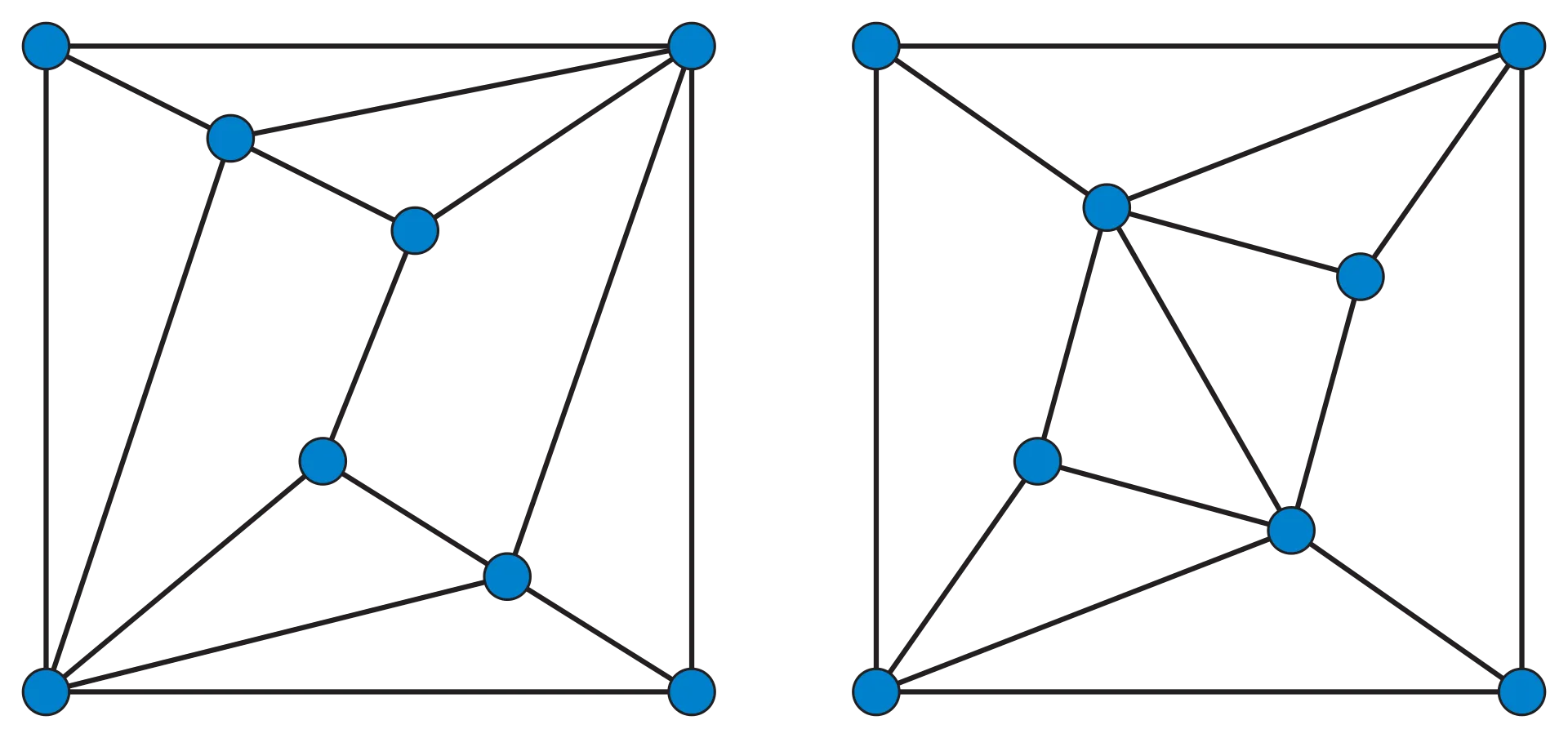
Cospectral graphs:
Two graphs are called cospectral or isospectral if the adjacency matrices of the graphs have equal multisets of eigenvalues.Cospectral graphs need not be isomorphic, but isomorphic graphs are always cospectral.
即上面两个图在空间域上肯定不是相等的两个图结构,但是在谱图域上这两个图结构具有相同的特征值的多集,因此它们称之为“共谱”或者“等谱”~
然后其他的这里就暂且不涉及了,首先明白在图模型中存在这样的一个概念就行了~
思想来源
首先结合之前我们看聚类的内容的时候,在DBSCAN那块有提及过,即DBSCAN是通过样本点之间的连通性(密度可达)来判断是否将样本聚为一类的,那个时候就提到过,需要注意这里在算法名称中的SC —— Spatial Clustering,是在空间域层面上的观察(只考虑在拓扑结构中的相对位置关系)。同理在谱聚类中,也考虑样本点之间的连通性。不过这里的连通性不是去判断两者之间是否相连,而是通过判断两者之间的链接是否可以断开。
聚类目标
在谱聚类中,主要是将数据样本看做是空间中的点,而这些点可以先进行边的补全,面对这样一个补全后的图结构,我们设定一种对于边的权重的定义公式,利用这个公式来对图进行划分,又称为切图。通过这样的操作,我们最终想要达到的目标是切图后的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
PS:这里我们来看一下~
DBSCAN的聚类方式是采用判断两个节点之间的连通性,通过定义搜索和判定的范围来实现,将节点聚合在一起,也就是说这里在实际操作的时候是一种自底向上的感觉,优先假设这些节点之间各自成为一个类别,然后向上聚合,最终达到一种聚集效果,在这个操作的实际过程中,这里只从一种空间上的距离关系进行了操作依据,因此是一种spatial上的聚类方式。
而再看谱聚类的聚类方式,是假设数据节点之间存在联通性,然后通过一种权重判断进行切图,类比DBSCAN聚类的方式,这里的实际操作其实是一种自顶向下的感觉,即优先假设这些节点全是一个类别,然后向下划分,最终达到一种聚集效果,在这个操作的实际过程中,存在了一种边的权重的判断,即我们可以理解为边的一种信息或者能量,因此这种聚类方式spectral上的聚类方式。
基础知识
OK~ 有了前面说的类比,我们知道了谱聚类的目标:权重和切图。为了实现这一目标,很显然我们需要定义一下权重如何计算,并且找到我们切图的依据。因此这里需要引入两个基础知识点:相似矩阵和无向图切图。但是为了明确这两个基础知识点还需要各自相应的铺垫。
无向权重图(For 相似矩阵)
图论中,对于一个图 $G$ 的定义一般是用两个集合来进行描述的,即 $G=(V,E)$ 。其中 $V$ 是数据集中所有的样本点,也是图定义中的点集合,$E$ 是这些样本点之间的边的集合,任意两个点之间既可以有边连接,也可以没有边连接,其连接就定义为 $w_{ij}$ ,若两个点之间存在连接则 $w_{ij} > 0$ ,否则的话记为 $0$ ,特别的在无向图之中,$w_{ij} = w_{ji}$ 。这个时候如果我们将节点间连接的情况用矩阵的形式表示出来的话,我们就得到了一个邻接矩阵 $W$,这个邻接矩阵是一个 $n \times n$ 的矩阵,其第 $i$ 行的第 $j$ 个值对应我们的权值 $w_{ij}$ 。
此外还引入一个度的概念,即对于图中任意一个点 $v_i$ ,它的度 $d_i$ 定义为和它相连的所有边的数量之和,即 $d_i = \sum_{j=1}^n w_{ij}$ ,即邻接矩阵中一横行的数据加起来之和。但是在这个时候我们无法将节点的度值放到前面定义的邻接矩阵中,因此又构造了一个只有对角线存在值得度矩阵,其中第 $i$ 行的第 $i$ 个值表示当前节点的度值,其他位置上的值均为零。
相似矩阵
虽然我们通过图论中得到了两个矩阵:邻接矩阵和度矩阵,但是我们该如何求出两两节点之间是否应该存在连接呢?通常我们可以在事先进行连接情况的定义,但是大多数情况下,我们都是只有数据点的本身,样本点没有办法直接给出这个邻接矩阵,那么此时我们该怎么得到这个邻接矩阵呢?
相信各位,首先映入脑海的一定是利用距离的定义,即如果我们定义一个距离计算方式来判断两个样本之间的远近程度,则可以将较近的一部分定义为连接,而较远的则定义为不连接。而这种方式就称为通过样本点距离度量的相似矩阵 $S$ 来获得邻接矩阵 $W$。
PS:显然这里如果我们只是将边之间的连接情况定义为了连接与不连接,但是这种情况能表达的信息还是过于少了,于是我们可以参考上面的思路,我们再假想一个权重矩阵,这个权重矩阵是对邻接矩阵中不为零的位置(即存在连接的情况),进行程度的判定,这个时候我们又得到了一个新的矩阵,但是仔细想一下,如果我们将这个矩阵和邻接矩阵对位相乘,就可以将这个定义出来的权重矩阵清除了掉了,同时也没有影响到邻接矩阵的基本定义,而是扩宽了其可以表达的内涵。
构造邻接矩阵的三类方法:
$\epsilon-$邻近法
对于 $\epsilon-$邻近法,它设置了一个距离阈值 $\epsilon$ ,然后用欧式距离公式 $s_{ij}$ 度量任意两点 $x_i$ 和 $x_j$ 的距离。即相似矩阵的 $s_{ij} = {\Vert x_i - x_j \Vert}_2^2$,然后根据 $s_{ij}$ 和 $\epsilon$ 的大小关系,来定义邻接矩阵 $W$ 如下: $$ w_{ij}= \begin{cases} 0& {s_{ij} > \epsilon} \\ \epsilon& {{s_{ij} \leq \epsilon}} \end{cases} $$
PS:从上式可见,两点之间的权重要不就是 $\epsilon$ ,要不就是 $0$ ,因此这个度量方式是极其不精确的。
$k-$邻近法
这种定义邻接矩阵的方式是,利用了先前的分类手段——KNN算法,来遍历所有的样本点,取每个样本最近的 $k$ 个点作为该点的近邻,只有和样本距离最近的 $k$ 个点之间的 $w_{ij} > 0$ 。但是这种方法会造成构造的邻接矩阵 $W$ 非对称的,为了解决这一个问题,一般有两种方式进行处理:
-
第一种:只要一个点在另一个点的 $k$ 近邻中,则两者之间的距离保留下来 $$ w_{ij}=w_{ji}= \begin{cases} 0& {x_i \notin \text{KNN}(x_j) ;and ;x_j \notin \text{KNN}(x_i)} \\ \exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in \text{KNN}(x_j); or; x_j \in \text{KNN}(x_i}) \end{cases} $$
-
第二种:必须两个点互为对方的 $k$ 近邻,两者之间的距离才保留下来 $$ w_{ij}=w_{ji}= \begin{cases} 0& {x_i \notin \text{KNN}(x_j) ;or;x_j \notin \text{KNN}(x_i)} \\ \exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in \text{KNN}(x_j); and ; x_j \in \text{KNN}(x_i}) \end{cases} $$
全链接法
这种方法,通过名字就明白其具体操作了,即它假设所有点之间的权重值都大于0,因此就需要引入一种函数,将两个样本之间的关联性定义出来,然后输出相应的权值。还记得之前在SVM算法中引入的核函数吗?有没有发现,那个时候我们引入的核函数,就是用来处理两两样本之间的关系,并且因为一步一步算计算量过于大,所以使用核函数可以直接得到我们想要结果,回想一下(那时我们说过哪些核函数?):多项式核函数、高斯核函数和Sigmoid核函数。还记得它们之间的特别之处吗?
PS:其他的点记不起来,就回头看下,这里直说一点,就是高斯核理论上可以产生无穷维的特征空间,即其会对样本点之间都定义相似性关系,因此最常使用的就是高斯核(RBF),此时邻接矩阵和相似矩阵就是同一个矩阵。
$$ w_{ij}=s_{ij}=\exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2}) $$
在实际使用中也是第三种最合理、最普遍~
拉普拉斯矩阵(For 切图)
拉普拉斯矩阵的定义实际上十分的简单,但是它却拥有很多很好地性质,这里我们只说后面内容中涉及到的性质,其余的性质在以后相关的地方会完善补全。
拉普拉斯矩阵:$L = D - W$ ,这里即度矩阵减去邻接矩阵,因为度矩阵只有对角线有值,而邻接矩阵有事对称矩阵,因此我们自然可以想到一些拉普拉斯矩阵优秀的性质:
-
拉普拉斯矩阵是对称矩阵,并且其所有的特征值是实数
-
对于任意的向量 $f$ ,我们有 $$ f^TLf = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2 $$
无向图切图
对于无向图 $G$ 的聚类角度来说,我们需要做的是将其进行切割,最终得到 $k$ 个相互之间没有连接的子图,它们满足 $A_i \cap A_j = \emptyset$ ,且 $A_1 \cup A_2 \cup … \cup A_k = V$。从最终的目的来说,我们需要对图进行切割,但是具体怎么操作呢?于是我们引入了下面两个概念:
- 对于任意两个子图点的集合 $A, B \subset V$,$A \cap B = \emptyset$ ,则我们定义 $A$ 和 $B$ 之间的切图权重为:
$$ W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij} $$
- 那么对于我们 $k$ 个子图点的集合:$A_1,A_2,..A_k$ ,我们定义切图为:
$$ \text{cut}(A_1,A_2,…A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}W(A_i, \overline{A}_i ) $$
有了如上两个定义,我们可以进行操作了,只要最小化 $\text{cut}(A_1,A_2,..A_k)$ 函数就可以了,但是实际操作之后发现了一些问题,如下图:
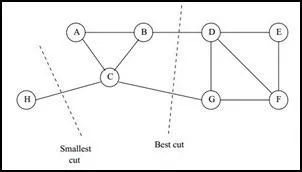
我们选择一个权重最小的边缘的点,比如 $C$ 和 $H$ 之间进行切割,这样虽然可以最小化我们的目标函数,但是却不是最优的图切割,因此我们还需要一些额外的补充条件,才能帮助我们求出最好的切割~
RatioCut切图
为了避免上面切图中的情况,因此立刻就能想到的解决方案就是,不光考虑最小化 $\text{cut}$ 目标函数最小化,还同时要考虑最大化每个子图中点的个数,即: $$ \text{RatioCut}(A_1,A_2,…A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{|A_i|} $$ 这里将子图中数量的大小引入到目标函数中,同时为了将子图中点的个数引入到目标函数中,将点数放到分母中,点数越大目标函数则越小以此达到了目的。接下来就要考虑如何最小化这个 $\text{RatioCut}$ 目标函数呢?
为了求解这个目标函数,我们引入指示向量 $h_j \in {h_1, h_2,..h_k}; j =1,2,…k$ ,对于任意向量 $h_j$ ,它是一个 $n$ 维向量($n$ 为样本数量),我们定义 $h_{ij}$ 为:
$$
h_{ij}= \begin{cases} 0& { v_i \notin A_j} \\ \frac{1}{\sqrt{|A_j|}}& { v_i \in A_j} \end{cases}
$$
那么我们对于 $h_i^TLh_i$ ,有:
$$
\begin{align}
h_i^TLh_i & = \frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^2 \\
& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{|A_i|}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{|A_i|}} )^2) \\
& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{|A_i|} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{|A_i|}) \\
& = \frac{1}{2}(\text{cut}(A_i, \overline{A}_i) \frac{1}{|A_i|} + \text{cut}(\overline{A}_i, A_i) \frac{1}{|A_i|}) \\
& = \frac{\text{cut}(A_i, \overline{A}_i)}{|A_i|}
\end{align}
$$
PS:看看我们得到了什么,$h_i^TLh_i=\frac{\text{cut}(A_i, \overline{A}_i)}{|A_i|}$ ,而考虑前面定义的 $\text{cut}$ 和 $\text{RatioCut}$ 两个定义表达式,即我们可以看出来 $\text{RatioCut} = h_i^TLh_i$
这里就引入了之前简单说的拉普拉斯矩阵的性质,通过其优秀的性质,我们可以看出,当对于某一个子图 $i$ ,它的 $\text{RatioCut}$ 对应于 $h_i^TLh_i$ ,那么我们的 $k$ 个子图呢?对应的 $\text{RatioCut}$ 函数表示为: $$ \text{RatioCut}(A_1,A_2,…A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = \text{tr}(H^TLH) $$ 有了这个结论之后,可以看出来,我们实际上的操作就变成了最小化 $H^TLH$ 矩阵的迹,又因为 $H$ 是我们引入的指示向量构成的矩阵,因此我们可以构造 $H^TH = I$ ,则我们最终切图的时候优化的目标就变为了: $$ \underbrace{\arg;\min}_H; \text{tr}(H^TLH) ;; s.t.;H^TH=I $$ 但是即使做到转换到这种地步,也不代表我们就能够求出最终的结果了,因为考虑到 $H$ 矩阵中每一个指示向量 $h_i$ 都是一个 $n$ 维的向量,向量中每一个变量的取值为 $0$ 或者 $\frac{1}{\sqrt{|A_j|}}$ ,这就有 $2^n$ 种情况,而我们需要有 $k$ 个子图的话,就有 $k$ 个指示向量,那么我们一共就有 $k·2^n$ 个备选 $H$ ,因此找到满足上面优化目标的 $H$ 就是一个 $NP$ 难的问题。
但是我们同时注意到 $\text{tr}(H^TLH)$ 中每一个优化子目标 $h_i^TLh_i$ ,其中 $h$ 是单位正交基,$L$ 为对称矩阵,此时 $h_i^TLh_i$ 的最大值为 $L$ 的最大特征值,最小值是 $L$ 的最小特征值。这里的思想跟后面的下一个章节中主成分分析法(PCA)的降维手段类似,在PCA中,我们的目标是找到一个协方差矩阵(对应此处的拉普拉斯矩阵 $L$)的最大特征值,而在谱聚类的这个过程中,我们的目标恰恰相反了,一是我们已经有了拉普拉斯矩阵,二是我们要找到对应的最小特征值。通过找到的最小的特征值,得到对应的特征向量,此时对应二分切图效果最佳。也就是说,我们这里要用到维度规约的思想来近似解决这个 $NP$ 难的问题。
对于 $h_i^TLh_i$ ,我们的目标是找到 $L$ 的最小特征值,而对于 $\text{tr}(H^TLH) = \sum\limits_{i=1}^{k}h_i^TLh_i$ ,则我们的目标是找到 $k$ 个这样的最小的特征值,一般来说,$k$ 肯定远远小于 $n$ ,也就是说通过维度规约,将维度从 $n$ 降到了 $k$ ,从而近似可以解决这个 $NP$ 难的问题。
通过找到的 $L$ 的最小的 $k$ 个特征值,可以得到对应的 $k$ 个特征向量,这 $k$ 个特征向量组成了一个 $n \times k$ 维度的矩阵,即为我们的 $H$ 。一般需要对 $H$ 矩阵按行做标准化,即 $$ h_{ij}^{*}= \frac{h_{ij}}{(\sum\limits_{t=1}^kh_{it}^{2})^{1/2}} $$ 由于我们在使用维度规约的时候损失了少量信息,导致得到的优化后的指示向量 $h$ 对应的 $H$ 现在不能完全指示各样本的归属,因此一般在得到$n \times k$ 维度的矩阵 $H$ 后还需要对每一行进行一次传统的聚类,比如使用K-Means聚类。
Ncut切图
$\text{Ncut}$ 切图和 $\text{RatioCut}$ 切图很类似,但是把 $\text{RatiocCut}$ 的分母 $|Ai|$ 换成了 $\text{vol}(A_i)$ 。这里的 $\text{vol}$ 表示样本的权重,由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说 $\text{Ncut}$ 切图优于 $\text{RatioCut}$ 切图。
$$
\text{Ncut}(A_1,A_2,…A_k) = \frac{1}{2}\sum\limits_{i=1}^{k} \frac{W(A_i, \overline{A}_i )}{\text{vol}(A_i)}
$$
对应的,$\text{Ncut}$ 切图也对指示向量 $h$ 进行了改进。注意到 $\text{RatioCut}$切图的指示向量使用的是 $\frac{1}{\sqrt{|A_j|}}$ 指示样本归属,而 $\text{Ncut}$切图使用了子图权重 $\frac{1}{\sqrt{\text{vol}(A_j)}}$ 来标识指示向量 $h$ ,定义如下:
$$
h_{ij}= \begin{cases} 0 & { v_i \notin A_j} \\ \frac{1}{\sqrt{\text{vol}(A_j)}}& { v_i \in A_j} \end{cases}
$$
而对于 $h_i^TLh_i$ 我们有:
$$
\begin{align}
h_i^TLh_i & = \frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^2 \\
& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{\text{vol}(A_i)}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{\text{vol}(A_i)}} )^2) \\
& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{\text{vol}(A_i)} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{\text{vol}(A_i)}) \\
& = \frac{1}{2}(\text{cut}(A_i, \overline{A}_i) \frac{1}{\text{vol}(A_i)} + \text{cut}(\overline{A}_i, A_i) \frac{1}{\text{vol}(A_i)}) \\
& = \frac{\text{cut}(A_i, \overline{A}_i)}{\text{vol}(A_i)}
\end{align}
$$
推导方式和 $\text{RatioCut}$ 完全一致。也就是说,我们的优化目标仍然是
$$
\text{Ncut}(A_1,A_2,…A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = \text{tr}(H^TLH)
$$
但是此时我们的 $H^TH \neq I$ ,而是 $H^TDH = I$ 。推导如下:
$$
h_i^TDh_i = \sum\limits_{j=1}^{n}h_{ij}^2d_j =\frac{1}{\text{vol}(A_i)}\sum\limits_{j \in A_i}d_j= \frac{1}{\text{vol}(A_i)}\text{vol}(A_i) = I
$$
也就是说,此时我们的优化目标变为了:
$$
\underbrace{\arg;\min}_H; \text{tr}(H^TLH) ;; s.t.;H^TDH=I
$$
此时我们的 $H$ 中的指示向量 $h$ 并不是标准正交基,所以在 $\text{RatioCut}$ 里面的降维思想不能直接用。这个时候,其实只需要将指示向量矩阵 $H$ 做一个小小的转换即可。我们令 $H = D^{-\frac{1}{2}}F$ ,则:$H^TLH = F^TD^{-1/2}LD^{-1/2}F$ ,$H^TDH=F^TF = I$,也就是说优化目标变成了:
$$
\underbrace{\arg;\min}_F; \text{tr}(F^TD^{-1/2}LD^{-1/2}F) ;; s.t.;F^TF=I
$$
可以发现这个式子就和 $\text{RatioCut}$ 基本一致,只是其中的 $L$ 变成了 $D^{-1/2}LD^{-1/2}$。这样就可以继续按照 $\text{RatioCut}$的思想进行求解问题了,即我们只需要求出 $D^{-1/2}LD^{-1/2}$ 的最小的前 $k$ 个特征值,然后求出其对应的特征向量,并标准化, 得到最后的特征向量 $F$ ,最后对 $F$ 进行一次传统的聚类(比如K-Means)即可。
PS:一般来说,$D^{-1/2}LD^{-1/2}$ 相当于对拉普拉斯矩阵 $L$ 做了一次标准化,即 $\frac{L_{ij}}{\sqrt{d_i*d_j}}$
算法流程
通过上面的基础知识的整理,我们可以看得出来谱聚类的基本流程中有几个关键的点:一是找出相似矩阵,二是进行切图,三是选择最后的聚类方法。最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式,最常用的切图方式是 $\text{Ncut}$ 。而到最后常用的聚类方法为 K-Means。下面以$\text{Ncut}$ 总结谱聚类算法流程。
输入:样本集 $D = (x_1,x_2,…,x_n)$ ,相似矩阵的生成方式为高斯核全连接方式,降维后的维度 $k_1$ ,聚类方法K-means,聚类后的维度 $k_2$ 。
输出:簇划分 $C = (c_1,c_2,…c_{k_2})$
- 根据输入的高斯核进行构建样本集的相似矩阵 $S$
- 根据相似矩阵 $S$ 构建邻接矩阵 $W$ ,构建度矩阵 $D$
- 计算出拉普拉斯矩阵 $L$
- 构建标准化后的拉普拉斯矩阵 $D^{-1/2}LD^{-1/2}$
- 计算 $D^{-1/2}LD^{-1/2}$ 最小的 $k_1$ 个特征值所对应的各自的特征向量 $f$
- 将各自对应的特征向量 $f$ 组成的矩阵按行标准化,最终组成 $n \times k_1$ 维的特征矩阵 $F$
- 对 $F$ 中的每一行作为一个 $k_1$ 维的样本,共 $n$ 个样本,用K-means进行聚类,聚类的维数为 $k_2$
- 得到最终的聚类结果 $C = (c_1,c_2,…c_{k_2})$
PS:后面的内容大篇幅的引用了刘建平老师的博文内容,看了几篇论文之后,发现还是刘老师总结的十分详细,相比论文中的晦涩的文字说明,还是更喜欢刘老师的表达~
![[读书笔记]《西瓜书》第九章 聚类](https://cdn.jsdelivr.net/gh/Ryuchen/ryuchen.github.io@master/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_700x350_resize_q75_box.jpg)