[读书笔记]《西瓜书》第七章 贝叶斯分类器 补充三

第七章 贝叶斯分类器 补充三

---

在前面一篇博文整理EM算法的时候，结尾是受限于篇幅所以戛然而止。

但是结尾处也是恰好的引入了ELBO（Evidence lower bound）的概念进来，对于ELBO的使用，更多的是在变分推断（variational inference）中，这一部分等到整理到第十四章的时候会详细的提到，感觉现阶段自己学习和整理的时候理解也不是很深入，相信随着时间推移届时可以整理更好的内容出来。

在西瓜书中对于近似推断的知识点，着重介绍了随机性推断中的基于采样的马尔可夫链蒙特卡罗（Markov Chain & Monte Carlo，简称MCMC）法。但是毕竟是一小节的内容，容纳的知识点和体量必然是有限的，参考《统计机器学习》一书和《深度学习》一书中，这个部分都是一个章的容量，于是借此机会拓展和整理一下相应知识点。

马尔可夫链蒙特卡罗法（MCMC）

本人在读到西瓜书这一节的时候感觉没读明白，于是翻了一下李老师的《统计学习方法》第十九章想作为学习的参考。结果却发现跟西瓜书一样，“啪”的一下直接甩了一脸模型和算法，“很快啊~”啥都没读的太懂，就结束了~ 这可不行啊，考虑到现在年轻人的基础太薄弱了啊，我劝这些作者“耗子尾汁”😝~

---

哈哈，皮了一下，主要其实还是自己太菜了，从根本上就没明白贝叶斯网的三个基本组成中的推断（inference）到底是用来做什么的，于是上网找了下shuhuai008大佬的视频看了下，发现也没有解答清楚自己的困惑，于是突然想到了，大佬在第一期视频中推荐的老师中有一名叫徐亦达的老师，于是在B站找了一下这个老师的视频。真是不找不知道，一看吓一跳啊，对于MCMC这一块专门有一个系列视频，解释的不要太详细，一下晋升成偶像级别的人物~

PS：这里感觉与看我整理的知识点，还不如去刷两遍老师的视频，链接放在下面~

PS：不过大家看不看，我都还是要整理的，毕竟这是我的笔记~

为什么要采样？

PS：首先声明一下，这个问题在花书《深度学习》一书中给出了答案，个人觉得大家看花书的内容就可以了，不过这里我还是要结合老师上课讲的内容整理一下。以下都是我个人学到的一些内容，不一定正确~

首先明确一个概念，贝叶斯网的任务组成主要是三个部分：结构、学习和推断。西瓜书的小章节内容组织的时候也是按照这样的结构进行总结的。于是，要解决标题提出的问题，我们首先要看它的前置问题：为什么要做推断？

西瓜书中给出的答案是：“贝叶斯网训练好之后就能用来回答‘查询’，即通过一些属性变量的观测值来推断其他属性变量的取值。”

PS：很浅显易懂的道理，不然我们费那么大劲学习贝叶斯网络干啥，对吧~

接下来给出了具体的定义：“这样通过已知变量观测值来推测待查询变量的过程称为‘推断’（inference），已知变量观测值称为‘证据’（evidence）”。

PS：定义给了出来，结合上面的“道理”也很好理解~

---

这一段我怎么没写在 知识整理的部分，是因为在这一章的铺垫内容中已经声明了一遍了~

---

接下来，结合徐老师在视频中说的，和西瓜书这一章开始的铺垫，我们可以总结出来一条结论~

“In many machine learning problems, you are actually interested in the posterior distribution $p(\theta|Data) \propto p(Data|\theta)p(\theta)$”

这里这个公式其实就是西瓜书中基于贝叶斯定理演化过来的，只不过省略了$p(Data)$，毕竟证据因子因为样本集的确定已经确定下来了，因此将等式转化为了正比公式。

PS：这里重新提两个知识点

• 点估计和先验分布：其实主要就是看你求 $\theta$ 的时候，是求解理想中的“best single $\theta$”，还是求解先验分布 “$p(\theta)$ the prior distribution of $\theta$ ”。
• $p(Data|\theta)$ 称为 似然（likelihood）；$p(\theta)$ 称为 先验（prior）；$p(\theta|Data)$ 称为 后验（posterior）

然后就是徐老师引入了共轭分布的知识点，不过现在我感觉下面的内容跟共轭没太大关系，就先不引入了，等下一段内容的时候再引入说明一下~

OK，得到上面的结论之后，我们可以看到，既然我们想通过贝叶斯网进行推断，那么本质上，我们其实就是在求解 $p(\theta|Data)$ 。结合前面朴素贝叶斯分类器的算法可以看出来，先验 $p(\theta)$ 大部分时候可以通过样本集或者前提假设的分布直接设定下来，而似然 $p(Data|\theta)$ 也可以通过训练集来确定，因此当我们有了上面那个正比公式之后，显然我们可以求解这么一个 $p(\theta|Data)$ 出来。

但是这个时候问题就来了，借助老师说的话：当 $p(\theta|Data)$ 的分布非常非常复杂的时候，我们就无法求解这个分布的性质了，像期望、最大值、方差等。于是这么看来，我们就无法进行推断（inference）了，毕竟在不知道分布性质的情况下，我们又如何能够做出有利于后续操作的推断呢，就像是：你在走迷宫一样，你可以对每一个路口都进行尝试，但是这样的操作又有什么意义呢？每条路都试一遍？那你求解模型干嘛呢，对吧~

PS：这个时候就不得不感慨前人的脑洞了，真的是NB，这个时候都能想出各种方式来近似求解~

此外透露一个小常识：走迷宫的时候，手放在左边的墙壁上，一直走下去，肯定能走出迷宫~

于是我们得到了我们的答案：MCMC就是求解这个后验分布的特性的一种方式~

PS：这里解决了《深度学习》中：为什么需要采样。这一小节中最开头的一句话：“有许多原因是我们希望从某个分布中采样。”这个结论的由来，后续具体的关于使用采样的原因，或者我更愿意称之为优点的部分，就参见花书就行了~

马尔可夫链蒙特卡洛采样的基础

明白了我们为什么使用采样的原因之后，在继续梳理蒙特卡洛相关的内容之前，保持我之前整理知识的一贯原则，我们首先要弄懂这样的一个方式前提假设，于是参考《深度学习》一书，补充一小节内容，蒙特卡洛采样的基础。

简单来说就两个需要掌握的内容：大数定理 和 中心极限定理。

PS：这里学过概率论与数理统计的人，应该已经掌握了，但是很不幸我就是学过了还没掌握的那个，于是重温一下，不过毕竟是配合这一章节的内容，所以也不会把全部内容都整理了，只整理涉及这一小节的内容。

首先是蒙特卡洛的思法前提是：通过估计数据的平均值来近似某分布下的期望。则我们可以得到两个公式：

$$ s = \sum_{\boldsymbol{x}} p(\boldsymbol{x})f(\boldsymbol{x}) = E_{p}[f(X)] $$

或

$$ s = \int_{\boldsymbol{x}}p(\boldsymbol{x})f(\boldsymbol{x})d\boldsymbol{x} = E_{p}[f(X)] $$

其中 $p(\boldsymbol{x})$ 是一个关于随机变量 $X$ 的概率分布（求和时）或者概率密度函数（求积分时）。

而在实际采样操作时，我们通过从 $p$ 中抽取 $n$ 个样本 $\boldsymbol{x}^{(1)}, ···, \boldsymbol{x}^{(n)}$ 来近似 $s$ 并得到一个经验平均值

$$ \hat{s}_n = \frac{1}{n} \sum_{i=1}^n f(\boldsymbol{x}^{(i)}) $$

OK，接下来就是引入相应知识的关键点了，因为我们需要证明这种近似的操作是合理的。

首先很容易观察到 $\hat{s}_n$ 这个估计是无偏的，由于

$$ \mathbb{E}[\hat{s}_n] = \frac{1}{n} \sum_{i=1}^n \mathbb{E}[f(\boldsymbol{x}^{(i)})] = \frac{1}{n}\sum_{i=1}^n s = s $$

然后需要证明如果样本 $\boldsymbol{x}^{(i)}$ 是独立同分布的，那么其平均值几乎必然收敛到期望值，即 $$ \lim_{n \rightarrow \infty} \hat{s}_n = s $$

PS：这里是值每次采样后都对样本进行求取经验平均值的操作，而这样的一个经验平均值的数列，必然会收敛到期望 $s$

这里就需要引入大数定理（Law of large number），这里只是考虑到蒙特卡洛的知识体系的完整性，所以补充的额外知识内容并不会完整~

大数定理（Law of large number）

定义

若 $\xi_1, \xi_2, ···, \xi_n$ 是随机变量序列，令 $\eta_n = \frac{\xi_1 + \xi_2 + ··· + \xi_n}{n}$ ，若存在常数序列 $a_1, a_2, ···, a_n$ 对任何的正数 $\varepsilon$ ，恒有 $$ \lim_{n \rightarrow \infty} P{|\eta_n - a_n| < \varepsilon } = 1 $$ 则称序列 ${\xi_n}$ 服从大数定律（或大数法则）

切比雪夫（Chebyishev）不等式：

设随机变量 $X$ 有数学期望 $E(X)$ 与方差 $D(X)$ ，则对任意的正数 $\varepsilon$ ，有 $$ P{|X-E(X)| \ge \varepsilon }\le \frac{D(X)}{{\varepsilon}^2} $$

三种大数定律

切比雪夫定理

设随机变量 $X_1, X_2, ···, X_n$ 相互独立，且具有相同的数学期望和方差： $$ E(X_k) = \mu \qquad D(X_k) = \sigma^2 $$ 则对任意的正数 $\varepsilon$ ，有 $$ \lim_{x \rightarrow \infty} P{|Y_n - \mu| < \varepsilon } = \lim_{n \rightarrow \infty} P{|\frac{1}{n}\sum_{k=1}^nX_k - \mu| < \varepsilon } = 1 $$

---

泊努利定理

设 $n_A$ 是 $n$ 次独立重复试验中事件 $A$ 发生的次数， $p$ 是事件 $A$ 在每次试验中发生的概率，则对任意的正数 $\varepsilon$ ，有 $$ \lim_{n \rightarrow \infty} P {|\frac{n_A}{n} - p| < \varepsilon } = 1 $$

---

辛钦定理

设 $X_1, X_2, …, X_n$ 相互独立，服从同一分布，具有数学期望 $E(X_k)=\mu$，则对任意正数，有 $$ \lim_{n \rightarrow \infty} P {| \frac{1}{n}\sum_{k=1}^n X_k - \mu | < \varepsilon } = 1 $$

中心极限定理

同分布的中心极限定理

设 $X_1, X_2, …, X_n$ 相互独立，服从同一分布，具有数学期望和方差: $$ E(X_k) = \mu \quad D(X_k) = \sigma^2 \neq 0 \quad (k=1,2,…,n) $$ 则对任意的 $x$ ，恒有 $$ \lim_{n \rightarrow \infty} F_n(x) = \lim_{n \rightarrow \infty} P { \frac{\sum_{k=1}^n X_k - n\mu}{\sqrt{n}\sigma} \le x } = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt $$

德莫弗-拉普拉斯定理

设随机变量 $\eta_n \quad (n = 1,2,…)$ 服从参数为 $n, p \quad (0<p<1)$ 的二项分布， $$ \lim_{n \rightarrow \infty} P { \frac{\eta_n - np}{\sqrt{np(1-p)}} \le x } = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt $$

蒙特卡洛采样

通过上面的基础铺垫，我们来看看到底什么是蒙特卡洛采样？在前面我们提到了通过贝叶斯定理，我们无论如何都是可以通过一定数量的样本集（似然），结合我们先前给的先验分布，求出我们目标的后验分布 $p(\theta|Data)$ 的表达式的。至此如果我们要对这个函数做任何的研究都应该是可行的，比如：如果我们对这个函数求解其期望的话，则 $$ \mathbb{E}_p[f] = \int f(x)p(x)dx $$ 因为函数中的 $x$ 服从概率分布 $p(x)$ ，但是这个时候如果 $f(x)$ 过于复杂，无法进行积分的操作怎么办？

因此结合前面的大数定律，假设我们可以从 $p(x)$ 中独立采样出 $L$ 个样本 $x^{(l)}, l=1,2,…,L$ ，那么我们可以近似的人为： $$ \mathbb{E}p[\hat{f}] = \frac{1}{L}\sum{l=1}^L f(x^{(l)}) $$ 而这就是我们常说的蒙特卡洛积分，基于该原理（用多个样本的均值来近似积分）的采样都称为蒙特卡洛采样。而如何从 $p(x)$ 中独立的取出 $L$ 个样本 $z^{(l)}$ 呢？这就诞生出了很多的采样方法了。

---

结合徐益达老师的视频里面的内容来看的，对采样方法的内容介绍大致分了三个部分： 1、基本采样法；2、马尔科夫蒙特卡洛采样法（M-H采样法和吉布斯采样法）；3、Slice Sampling（这篇博文就不记录这个采样了，具体这个采样可以参见徐益达老师的视频~）

如果你觉得上面的描述还是有点抽象的话，除了网上找到的资料和徐老师课上讲的内容，还有一种对于蒙特卡洛采样的可视化总结，远比上面要易懂的多，如下：

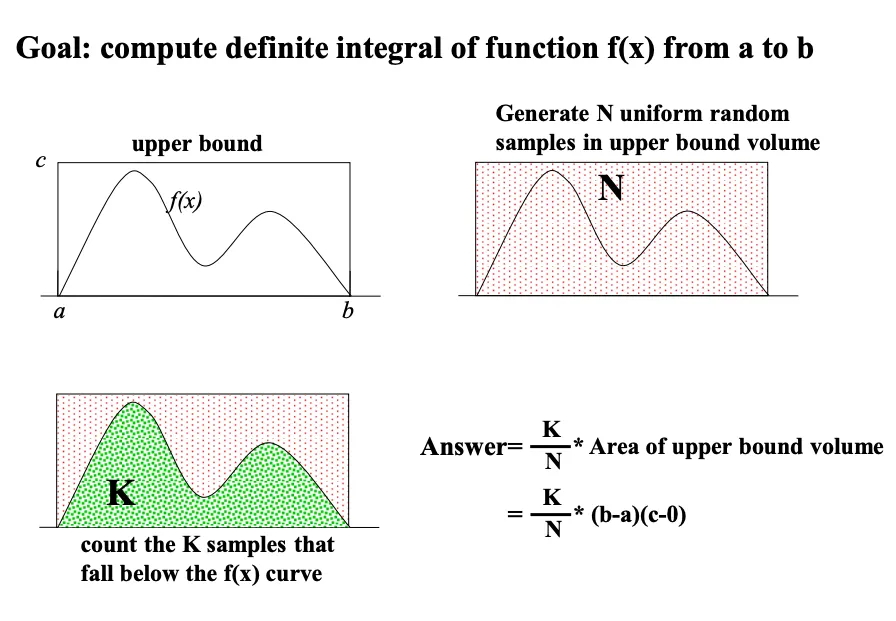
怎么样，这种图示是不是一眼就清楚具体蒙特卡洛的思想是什么了？

基本采样法

几乎所有的基本采样方法都是以均匀分布随机数作为基本变换操作的。

Box-Muller 变换

如果随机变量 $U_i, U_2$ 独立且 $U_1, U_2 \sim Uniform[0,1]$ ， $$ Z_0 = \sqrt{-2 \ln U_1}\cos(2\pi U_2) $$

$$ Z_1 = \sqrt{-2\ln U_1}\sin(2\pi U_2) $$

则 $Z_0, Z_1$ 独立且服从标准正泰分布。

其它几个著名的连续分布，包括指数分布、Gamma分布、t-分布、F-分布、Beta分布、Dirichlet分布等等，也都可以通过类似的数学变换得到；离散的分布通过均匀分布更加容易生成。在 python 的 numpy，scikit-learn 等类库中，都有生成这些常用分布样本的函数可以使用。

不过当 $p(x)$ 的形式很复杂，或者 $p(\boldsymbol{x})$ 是个高维的分布的时候，样本的生成就可能很困难了。譬如有如下的情况：

• $p(x) = \frac{\hat{p}(x)}{\int\hat{p}(x)dx}$， $\hat{p}(x)$ 我们可以得到，但是下面的积分我们无法得到显式解（归一化系数很难计算）；
• $p(x,y)$ 是一个二维的分布函数，这个函数本身计算很困难，但是条件分布 $p(x|y), p(y|x)$ 的计算相对简单；如果 $p(\boldsymbol{x})$ 是高维的，这种情形就更加明显。

---

PS：下面介绍几种常见的基本采用方法，内容和定义的主要来源为 wikipedia。

逆变换采样（Inverse Transform Sampling）

假设 $X$ 为一个连续随机变量，其累积分布函数为 $F_X$ 。此时，随机变量 $Y=F_X(X)$ 服从区间 [0, 1] 上的均匀分布。逆变换采样即是将该过程反过来进行：首先对于随机变量 $Y$，我们从 0 至 1 中随机均匀抽取一个数 $u$。之后，由于随机变量 $F_X^{-1}(Y)$ 与 $X$ 有着相同的分布， $x = F_X^{-1}(u)$ 即可看作是从分布 $F_X$ 中生成的随机样本。

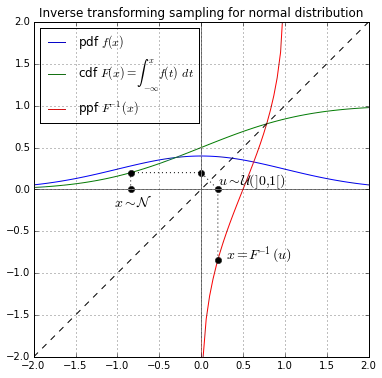
由Olivier Ricou - 自己的作品，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=42827656

example

假设有一个累积分布函数CDF $$ F(x) = 1 - \exp(-\sqrt{x}) $$ 我们要从该分布中生成随机样本。$F(x)$ 的反函数为： $$ \begin{align} F(F^{-1}(u)) & = u \\
1 - \exp \left( -\sqrt{F^{-1}(u)} \right) & = u \\
F^{-1}(u) & = (-\log(1-u))^2 \\
& = (\log(1 - u))^2 \end{align} $$ 于是，我们先从 0 至 1 中随机均匀抽取 $u$ ，然后计算 $F^{-1}(u) = (\log(1 - u))^2$ 以得到我们需要的样本

我们可以看出来逆变换采样的方法确实有效，但是有一个非常严格的要求就是对应分布函数的CDF必须能够通过对PDF积分求出来，并且这个CDF函数还是要能够求解逆函数的，因此这样的采样方式虽然非常方便，但是适用范围太窄了。

拒绝采样（Rejection Sampling）

拒接采样，也通常被称为接受采样，或者拒绝-接受采样等，其对应的基本思想：假设我们想对 PDF 为 $p(x)$ 的函数进行采样，但是由于种种原因，对其进行采样是十分复杂困难的。但是另一个 PDF 为 $q(x)$ 的函数相对容易采样。那么，当我们将 $q(x)$ 与一个常数 $k$ 相乘以后，可以实现下图所示的关系，即 $k·q(x)$ 将 $p(x)$ 完全“覆盖”。

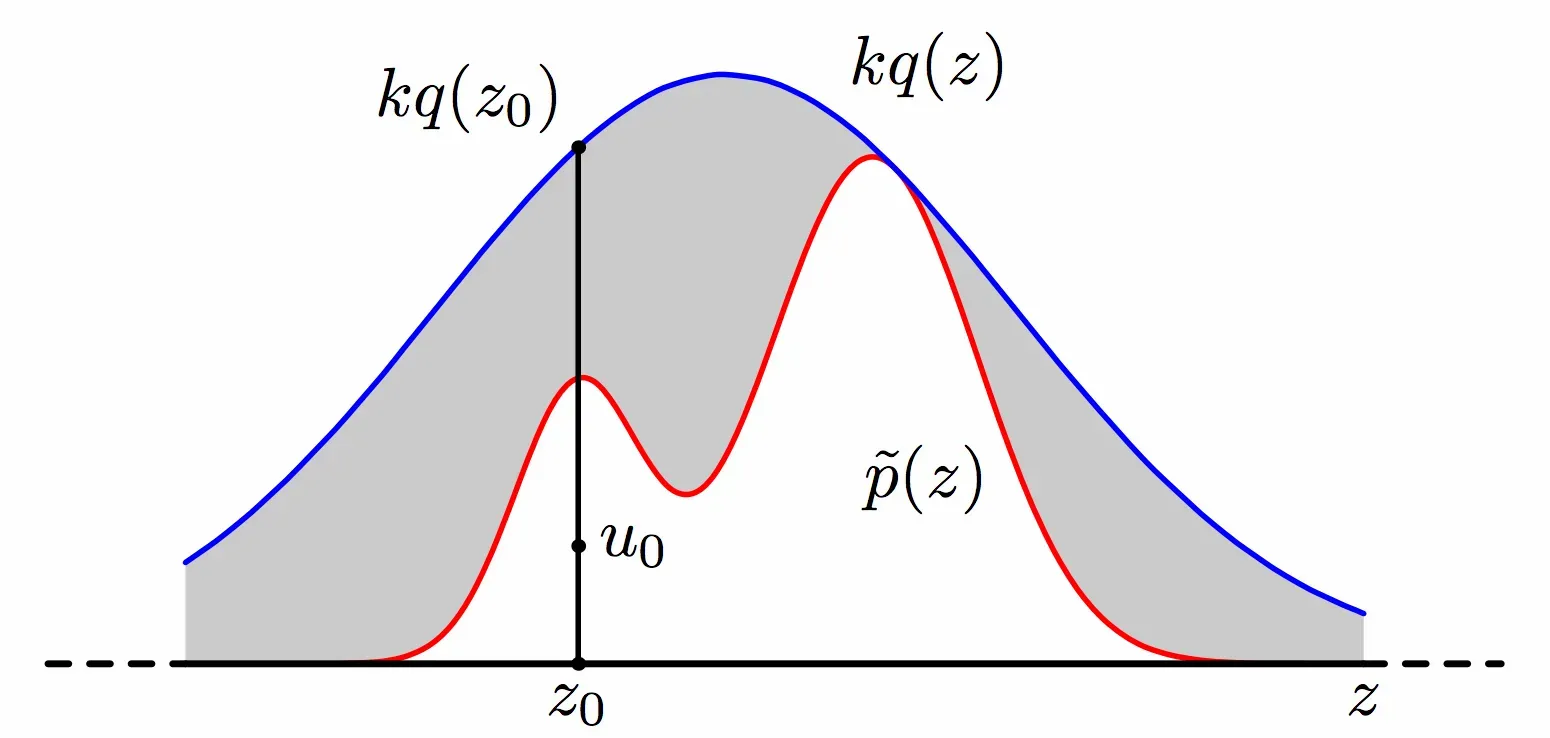
PS：这里之所以乘以 $M$ 是因为 PDF 函数是的积分都是 1 ，因此不可能两个概率密度函数不可能完全覆盖~

然后重复如下步骤，直到获得 $m$ 个被接受的采样点：

• 从 $q(z_0)$ 中获得一个随机采样点 $z^{(i)}$
• 从均匀分布 $[0, kq(z^{(i)})]$ 中随机采样 $u_0$ 点
• 若 $u_0 > \hat{p}(z_0)$ ，则拒绝样本 $z_0$，否则接受样本 $z_0$
• 重复 1 ~ 3 步骤，所有接受样本 $z$ 的集合可以认为是从分布 $p(z)$ 独立采样出的样本集合

PS：为了提高采样的效率（降低拒绝样本出现的概率），我们应该尽可能地选取靠近 $p(z)$ 的分布函数

由此我们可以计算出一个样本被接受的概率 $$ p_{accept}(z) = \int \frac{\hat{p}(z)}{kq(z)} q(z)dz = \frac{1}{k}\int \hat{p}(z)dz $$ 即在符合条件 $kq(z) \ge \hat{p}(z)$ 的条件下，$k$ 越小，样本被接受的概率越大。

PS：这里可以看出来拒绝采样的想法与蒙特卡洛积分的一致性

我们可以看到拒绝接受采样很好地避免了逆变换采样的局限性，但是由于在采样的过程中引入了拒绝和接受的动作，因此引入了额外的开销，而且这个开消会因为 $k$ 的选择而浮动。

重要性采样 (Importance sampling)

在重要性采样中我们与拒绝采样一样，同样引入一个 PDF为 $q(z)$ 的函数，这次对其的值域不进行乘以系数以扩大，而是将通过 $q(z)$ 得到的样本，全部接受。然而，通过 $q(z)$ 采样出的样本显然不符合原本的 $p(z)$ 分布，为了矫正这个偏差，我们给每个样本附一个重要性权重，比如使 $\frac{p(z_0)}{q(z_0)} = 1$ 的样本权重较大，使 $\frac{p(z_0)}{q(z_0)} = 0.1$ 的样本权重较小。

PS：很容易就行联想到 $\frac{p(z_0)}{q(z_0)}$ 自身就是一个很好的权重表示

$$ \mathbb{E}[f] = \int f(z)p(z)dz = \int f(z) \frac{p(z)}{q(z)}q(z)dz \approx \frac{1}{L} \sum_{l=1}^L f(z^{(l)})\frac{p(z^{(l)})}{q(z^{(l)})} = \sum_{l=1}^L w_l f(z^{(l)}) $$

PS：这里可以看出来重要性采样其实主要是用来分析原始分布的期望，那么我们如何通过重要性采样来获得原始分布呢？

这里我们可以通过重采样（resampling）的方式，通过将重要性采样的样本集中再采样出原始分布下的样本数据。

• 从分布 $q(z)$ 中采样 $L$ 个样本 $z^{(1)}, z^{(2)}, …, z^{(L)}$
• 计算每个样本点 $z^{(l)}$ 的权重 $\frac{p(z^{(l)})}{q(z^{(l)})}$
• 将计算出的权重归一化 $w_1, w_2, …, w_L$ 从样本集 $z^{(1)}, z^{(2)}, …, z^{(L)}$ 中随机采样 $M$ 个样本 $\hat{z}^{(1)}, \hat{z}^{(2)}, …, \hat{z}^{(M)}$
• 当 $M \rightarrow \infty$ 时，样本 $\hat{z}^{(1)}, \hat{z}^{(2)}, …, \hat{z}^{(L)}$ 为服从 $p(z)$ 分布的样本集

---

总结一下，以上三个基本采样法就是采用蒙特卡洛思想的采样方法也是最具代表性的三个采样方法，其中重要性采样法在其他模型中也都有使用，例如接下来在集成学习那一章当中，我们要使用bootstrap方法也包含了重要性采样的思想在里面~

马尔科夫链蒙特卡洛采样法

马尔科夫链蒙特卡洛 （Marko chain Monte Carlo）同样也是采用建议分布（proposal distribution），即 $\pi(z)$，来进行采样。与前面介绍的方法不同的是，MCMC的采样过程与采样序列相关，即其 proposal distribution 与当前采样样本相关：$$\pi(z|z^T)$$。

就MCMC采样的整体框架而言，个人感觉还是徐亦达老师说的比较清楚~

在徐亦达老师的视频中，老师做了这样的一个图，首先我们采样过程中的样本是根据马尔科夫性质得到的，则每一个样本都是由前一个样本通过转移概率得来，即 $k(x^{t-1} \mapsto x^t)$ ，而这些样本必然要符合样本原先得到的分布函数即 $q(x)$ ，因此通过 转移概率 $k(x^{t-1} \mapsto x^t)$ 得到的 $\pi(x)$ 与 $q(x)$ 两者之间是近似相等的。而这个时候问题的求解就不再是找出 $\pi(x)$，而是要找出 $k(x^{t-1} \mapsto x^t)$。

即通过马氏链的平稳分布来作为我们的建议分布（proposal distribution），因此问题的关键是求解这个平稳分布 $\pi(x)$。

PS：马氏链的平稳分布的得来在下文中就补充进来~

$$ \pi_t(x^*) = \int \pi_{t-1}(x)k(x \mapsto x^*)dx $$

而因为 $\pi_t$ 与 $\pi_{t-1}$ 是我们要求的同一种分布，因此这个表达式可以直接表示为 $$ \pi(x^*) = \int \pi(x)k(x \mapsto x^*)dx $$ 但是这个公式很难求解，因此转而求解另一个关键方程——detailed balance $$ \pi(x)k(x \mapsto x^*) = \pi(x^*)k(x^* \mapsto x) $$ 或 $$ \pi(x)k(x^*|x) = \pi(x^*)k(x|x^*) $$ 这个其实很好理解，其实就是忽略了前后关系，然后反复横跳，两两之间横跳过程中得出的概率一定是相等的。更进一步理解的话，可以看出马尔科夫链的样本一定是满足这个条件的，但是满足这个条件的不一定是马尔科夫链，因此这个条件是马尔科夫链的充分条件，而非必要条件。

证明一下就是：

$$ \begin{align} \pi(x^*) & = \int \pi(x)k(x \mapsto x^*)dx \\
& = \int \pi(x^*)k(x^* \mapsto x)dx \quad (\text{带入了detailed balance condition})\\
& = \pi(x^*)\int k(x^* \mapsto x)dx \\
& = \pi(x^*) \end{align} $$

---

马尔科夫链（Marko Chain）

在阐述马尔科夫链之前，首先还是一贯的基础基调，我们得先明白什么是马尔科夫性质。

马尔科夫性质是概率论中的一个概念，当一个随机过程在定现在状态以及所有过去状态下，其未来状态的条件概率分布仅依赖于当前状态；换句话说，在给定现在状态时，它与过去状态（即该过程的历史路径）是条件独立的，那么此随机过程即具有马尔科夫性质。 —— quote from wikipedia

具有马尔可夫性质的过程通常称之为马尔可夫过程。

在概率论及统计学中，马尔可夫过程（英语：Markov process）是一个具备了马尔可夫性质的随机过程，因为俄国数学家安德雷·马尔可夫得名。马尔可夫过程是不具备记忆特质的（memorylessness）。换言之，马尔可夫过程的条件概率仅仅与系统的当前状态相关，而与它的过去历史或未来状态，都是独立、不相关的。 —— quote from wikipedia

由波兰语维基百科的Xpicto，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=8496061

而具备离散状态的马尔科夫过程，通常被称为马尔科夫链。马尔科夫链通常使用离散的时间集合定义，又称离散时间马尔科夫链。

PS：总结一句：相信大家一定听过那句话，给定现在，过去与未来条件独立~

马尔科夫链定理

如果给定一个非周期马氏链具有转移概率矩阵 $P$ ，且它的任何两个状态都是连通的，那么 $\lim_{n \rightarrow \infty} P_{ij}^{n}$ 存在且与 $i$ 无关，记 $\lim_{n \rightarrow \infty} P_{ij}^n = \pi(j)$ ，我们有： $$ \lim_{n \rightarrow \infty} P^n = \begin{bmatrix} \pi(1) & \pi(2) & ··· & \pi(j) & ··· \\
\pi(1) & \pi(2) & ··· & \pi(j) & ··· \\
··· & ··· & ··· & ··· & ··· \\
\pi(1) & \pi(2) & ··· & \pi(j) & ··· \\
··· & ··· & ··· & ··· & ··· \\
\end{bmatrix} $$ $\pi(j) = \sum_{i=0}^\infty \pi(i)P_{ij}$，$\pi$ 是方程 $\pi P = \pi$ 的唯一非负解，其中 $$ \pi = [\pi(1), \pi(2), …, \pi(j), …]，\sum_{i=0}^\infty \pi_i = 1 $$ $\pi$ 称为马氏链的平稳分布。

上面的性质中需要解释的有：

• 非周期的马尔科夫链：这个主要是指马尔科夫链的状态转化不是循环的，如果是循环的则永远不会收敛。幸运的是我们遇到的马尔科夫链一般都是非周期性的。用数学方式表述则是：对于任意某一状态 $i$ ，$d$ 为集合 ${n|n \ge 1, P_{ii}^n > 0}$ 的最大公约数，如果 $d=1$ ，则该状态为非周期的

• 任何两个状态是连通的：这个指的是从任意一个状态可以通过有限步到达其他的任意一个状态，不会出现条件概率一直为 0 导致不可达的情况。

• 马尔科夫链的状态数可以是有限的，也可以是无限的。因此可以用于连续概率分布和离散概率分布。

• $\pi$ 通常称为马尔科夫链的平稳分布。

PS：注意，这里的 $\pi$ 其实不就是我们要求的分布吗？

---

Metropolis-Hastings采样

PS：关于MH采样算法和Gibbs采样网上的资料一大堆，不过我个人还是觉得跟着徐老师的视频看它的课件理解的更好~

下面的内容也就以徐老师的课件为主

在前面理解了MCMC的整体框架之后，我们再看MH算法就会发现，其在整体框架的下面，加入了一个接收函数，而这个函数就是上面截图中的 $\min(1, \frac{\pi(x^*)q(x|x^*)}{\pi(x)q(x^*|x)})$。

然后算法下面给了两点：

• 如果得到的值小于采样的 $u$ ，则重复当前的这个样本
• 如果一个样本重复太多次，则这个分布不够好

Why it work ?

首先要证明这个采样方法是有效的话，则我们首先想到的就是 detailed balance 条件，因此我们先看 $k(x \mapsto x^*)$ 是什么~

$k(x \mapsto x^*)$ 包含了两个部分的：

• $x^*$ 从原始分布 $q(x)$ 中被采样出来的概率 $q(x^*|x)$
• 这个 $x^*$ 被接收的概率 $\alpha_{accept}(x^*, x) = \min(1, \frac{\pi(x^*)q(x|x^*)}{\pi(x)q(x^*|x)})$

将这两个带入到 detailed balance 的公式中 $$ \begin{align} \pi(x)q(x^*|x)\alpha(x^*, x) & = \pi(x)q(x^*|x)\min(1, \frac{\pi(x^*)q(x|x^*)}{\pi(x)q(x^*|x)}) \\
& = \min(\pi(x)q(x^*|x), \pi(x^*)q(x|x^*)) \\
& = \pi(x^*)q(x|x^*)\min(1, \frac{\pi(x)q(x^*|x)}{\pi(x^*)q(x|x^*)}) \\
& = \pi(x^*)q(x|x^*)\alpha(x, x^*) \end{align} $$ 可见 detailed balance 的条件是符合的，但是需要注意的是，在这里 $\alpha(x^*, x) \neq \alpha(x, x^*)$

Gibbs 采样

Gibbs 采样本身是属于一次一次迭代操作，并不能进行并行操作，但是有一个统计学上的手段可以进行并行操作

其实 Gibbs采样 本身很好理解，针对多变量的情况下，在固定其余变量的情况下，采样另一个变量，接下来就是要证明其的有效性，这里参考之前的 MH采样 的思路应该是要证明detailed balance，但是徐亦达老师给了一个思路，就是不需要证明detailed balance，只要证明 Gibbs采样 是 MH采样 的一个特例就行了~

PS：这里徐老师是通过拓展 MH采样 中的接收率变化为什么来看 Gibbs采样 的

其中 $-k$ 下标表示除了第 $k^{th}$ 这个元素

当我们已经通过 Gibbs采样 方法，采样得到了 $\boldsymbol{x} = x_1, x_2, …, x_D$ 这个样本，于是回头看的时候，假设我们当前正在采样这第 $k^{th}$ 个维度，因为我们采样的时候除了 $k^{th}$ 这个维度，其他的维度分量是不变的，因此 $\boldsymbol{x}^*_{-k} = \boldsymbol{x}_{-k}$ 。而在MH算法中的$q_k(\boldsymbol{x}|\boldsymbol{x}) = \pi(\boldsymbol{x}^*_k|\boldsymbol{x}_{-k})$，因此有了上述的方程。即带入到MH算法中的 $\alpha$ 中，最终 Gibbs采样 可以看做是，在接收率恒等于 1 的情况下的 MH采样~