[读书笔记]《西瓜书》第七章贝叶斯分类器补充二

December 22, 2020

3804 17 minutes and 17 seconds

第七章贝叶斯分类器补充二

简略的整理完“判别式模型”和“生成式模型”之后，下面要补充的部分就是西瓜书第七章末节提到的EM算法了。还记得这个对于这个算法的第一次接触，是在一个机缘巧合的情况下，帮外国的同学解决他们的课后作业中在CV处理领域中接触到的EM算法，但是当时只是粗略的领略了一下。不过在后来学习过程中，小组内部会议讨论高斯混合模型（Gaussian mixture model）的时候认真学了一下。所以感觉西瓜书中对于EM算法的简述还是过于简单了，相对比李航老师的统计机器学习来说。接下来就整理一下自己所搜集到的全部的相关资料~

PS：主要是围绕着shuhuai008大佬的视频和网上比较有名的一篇斯坦福的文章《What is the expectation maximization algorithm?》

最大期望算法（Expectation Maximization）

西瓜书中引入EM算法是在介绍完贝叶斯网之后，借由部分可观测的现象来简要的介绍了该算法的主要概念，即无法直接求解极大似然时，使用估计的方式来推断含有隐变量时的概率模型参数的极大似然估计法~

当然短短的一小节并不能看透其内容，而且这里因为引入的西瓜例子，个人感觉对于隐变量的解释有点使读者产生片面的错觉。书中前面的内容一直都是相关的西瓜可观测的变量（根蒂、花纹、颜色等等），但是这里介绍部分可观测时，说的是“根蒂已经掉落”，这里个人理解是数据的缺失，而非部分可观测的解释~

PS：不知道自己的理解对不对，但是感觉对比李航老师的《统计机器学习》一书来看对于隐变量的解释——经典三硬币，西瓜书这里的解释是有问题的~

说了这么多，接下来还是要从头开始梳理相关内容~

什么是EM算法？

无论是从《统计学习方法》还是西瓜书中，我们都得知EM算法是一种迭代算法，主要是用于求解含有隐变量的概率模型参数的极大似然估计算法，或极大后验概率估计算法。其每次迭代主要由两步组成：E步（Expectation Step）和M步（Maximization Step）。但是这样的认识显然是浅薄的，因此我找了一下维基百科的解释引用在下：

In statistics, an expectation–maximization (EM) algorithm is an iterative method to find (local) maximum likelihood or maximum a posteriori (MAP) estimates of parameters in statistical models, where the model depends on unobserved latent variables. The EM iteration alternates between performing an expectation (E) step, which creates a function for the expectation of the log-likelihood evaluated using the current estimate for the parameters, and a maximization (M) step, which computes parameters maximizing the expected log-likelihood found on the E step. These parameter-estimates are then used to determine the distribution of the latent variables in the next E step. —— quote by wikipedia

通过上面维基百科的解释，我们可以看到EM算法中有两点是特别重要的信息，其中一点跟前面两本机器学习书籍中的描述一致，就是EM算法是求解含有latent variables的极大似然估计算法，另一点是两本书中都没有提及的，即其求解的也是局部的极大，并非全局最优。

PS：这里先按下不表，后面再进行说明~

核心公式

通过前面的描述和定义，我们知道了通常的极大似然估计的核心公式就是: $$ \theta_{MLE} = \underset{\theta}{\arg\max} \log P(X|\theta) $$ 而在引入了隐变量之后的极大似然估计之后，其核心公式则变成了： $$ \theta^{t+1} = \underset{\theta}{\arg \max} \int_{z} \log P(X,Z|\theta)P(Z|X,\theta^t)dZ $$

PS：这里引用的是shuhuai008的视频中的写法

西瓜书中的表达为 $$ \Theta^{t+1} = \underset{\Theta}{\arg\max} \mathbb{E}_{Z|X,\Theta^t}[LL(\Theta|X,Z)] $$ 统计机器学习中的表达为 $$ \theta^{i+1} = \underset{\theta}{\arg\max}\mathbb{E}_Z[\log P(X,Z|\theta)|X, \theta^i] $$ 虽然表示不同，但是表达的意思是一样的，而且化简大家都一样~

这里 $X$ 表示观测随机变量的数据， $Z$ 表示隐随机变量的数据。 $X$ 和 $Z$ 和在一起称之为完全数据（complete-data）

算法描述

输入：观测变量数据 $X$，隐变量数据 $Z$ ，联合分布 $P(Y,Z|\theta)$ ，条件分布 $P(Z|Y, \theta)$

输出：模型参数 $\theta$

过程：

选择参数的初值 $\theta^0$ ，开始迭代；
$E$ 步：记 $\theta^i$ 为第 $i$ 次迭代参数 $\theta$ 的估计值，在第 $i+1$ 次迭代的 $E$ 步，计算

$$ Q(\theta,\theta^i) = E_Z[\log P(X,Z|\theta)|X,\theta^i] = \sum_Z \log P(X,Z|\theta)P(Z|X,\theta^i) $$

$M$ 步：求使 $Q(\theta,\theta^i)$ 极大化的 $\theta$ ，确定第 $i+1$ 次迭代的参数的估计值 $\theta^{i+1}$

$$ \theta^{i+1} = \underset{\theta}{\arg\max} Q(\theta, \theta^i) $$

重复第上面 $E$ 步和 $M$ 步，直到收敛。

PS：下面关于 $EM$ 算法作几点说明：

参数的初值可以任意选择，但需注意 $EM$ 算法对初值是敏感的

给出停止迭代的条件，一般是较小的正数 $\varepsilon$ ，若满足 $\Vert \theta^{i+1} - \theta^i \Vert \le \varepsilon$ 或 $\Vert Q(\theta^{i+1},\theta^i) - Q(\theta^i, \theta^i) \Vert \le \varepsilon$ ，则停止迭代。

举个例子

PS：这里就不摘抄三个硬币的经典例子了，而是使用《What is the expectation maximization algorithm?》一文中给出的例子

最大似然估计

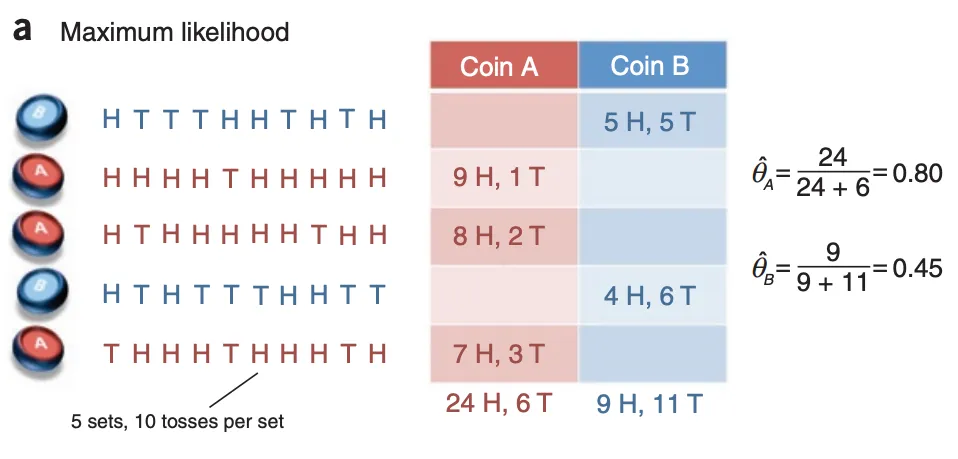
EM算法估计

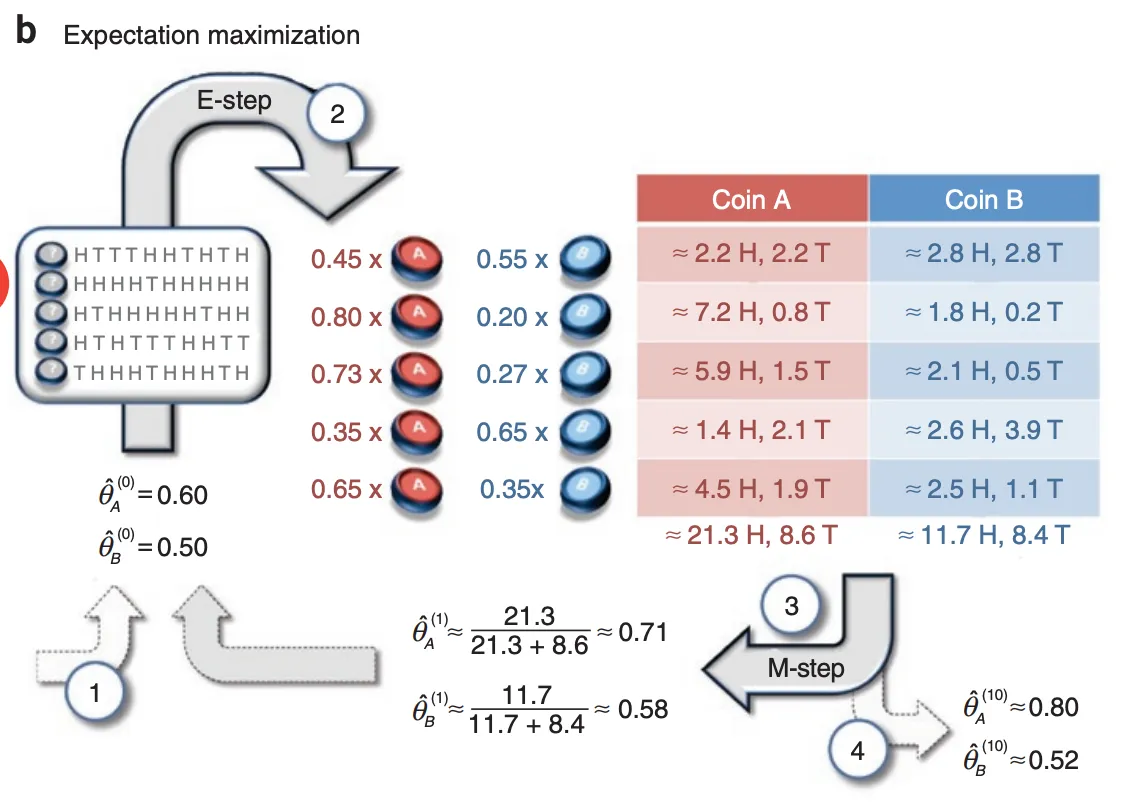
通过文中这两幅图的表达，可以清晰地认识到，在 a 图中使用最大似然估计来推测A硬币和B硬币的正反概率（或者理解成硬币的质量分布）时，其是对两个硬币进行单独的估计的，而在 b 图中使用EM算法估计时，因为隐变量——不知道当前的硬币是来自A还是B，所以是两个硬币的一起估计。

简单概述下 b 图的执行过程：

首先初始化设置我们的模型参数 $\theta^a$ 和 $\theta^b$ 的值

在 $E$ 步中根据设置的 $\theta^a$ 和 $\theta^b$ 来推测硬币A和硬币B的概率分布，然后根据这个分布来生成当前预测 head 和 tail 的数量

在 $M$ 步中根据当前生成的预测结果数量，来重新计算 $\theta^a$ 和 $\theta^b$ 的值

重复 $E$ 步和 $M$ 步，当迭代趋于收敛后，结束当前循环，输出当前 $\theta^a$ 和 $\theta^b$ 的值

为什么有效？

期望最大化算法是对不完整数据情况下的求解最大似然估计的一种自然的概括。（PS：这里个人理解为，既然这样的现象出现了，则其出现的可能性一定是最大的，因此模型参数使得该现象出现的概率应该是最大的，即最大似然）一般而言，期望最大化算法解决的优化问题要比最大似然估计对应的优化问题困难的多。在完整数据下，目标函数 $\log P(X,Z|\theta)$ 具有单个全局最优值，通常可以通过闭式解的形式求解得到。与之相反的是，在不完全数据下，$\log P(X|\theta)$ 具有多个局部极大值，因此无法通过闭式解的方式求得最大值。

为了解决这个问题，期望最大化算法将优化 $\log P(X|\theta)$ 的艰巨任务简化为一系列更简单的优化子问题，这些子问题的目标函数具有唯一的全局最大值，通常可以以闭式解的形式对其进行求解。子问题的选择方式则是能保证它们在相应的条件下可以求得 $\theta^1$，$\theta^2$，…，并且它们的这些解会收敛到 $\log P(X|\theta)$ 的局部最优值。因此每一次迭代中的 $E$ 步和 $M$ 步都是在做相应的子问题生成与求解的过程，那么对应的收敛性则如何保证？

收敛性

即求证： $$ \theta^t \rightarrow \theta^{t+1}, \log P(X|\theta^t) \le \log P(X|\theta^{t+1}) $$

PS：这里引用shuhuai008大佬的视频中的证明过程

首先第一步是转换 $$ \log P(X|\theta) = \log \frac{P(X,Z|\theta)}{P(Z|X,\theta)} = \log P(X,Z|\theta) - \log P(Z|X,\theta) $$ 两边同时对 $P(Z|X,\theta^t)$ 同时求期望

左边： $$ \begin{align} & = \int_Z P(Z|X,\theta^t) \log P(X|\theta) dZ \\
& = \log P(X|\theta) \int_Z P(Z|X,\theta^t)dZ \\
& = \log P(X|\theta) \end{align} $$

PS：因为这里积分里只跟 $Z$ 有关，因此积分等于1

右边： $$ = \int_Z P(Z|X,\theta^t) \log P(X,Z|\theta)dZ - \int_Z P(Z|X,\theta^t)\log P(Z|X,\theta)dZ $$ 令前一项为 $Q(\theta, \theta^t)$ ，后一项为 $H(\theta, \theta^t)$

则仅需证明 $$ Q(\theta^{t+1}, \theta^t) \ge Q(\theta^t, \theta^t)，H(\theta^{t+1}, \theta^t) \le H(\theta^t, \theta^t) $$

PS：这里只证明一个，另一个同理

$$ \begin{align} & H(\theta^{t+1},\theta^t) - H(\theta^t, \theta^t) \\
= & \int_Z P(Z|X,\theta^t) \log P(Z|X,\theta^{t+1})dZ - \int_Z P(Z|X,\theta^t) \log P(Z|X,\theta^t)dZ \\
= & \int_Z P(Z|X, \theta^t) \log \frac{P(Z|X,\theta^{t+1})}{P(Z|X,\theta^t)} dZ \\
= & - KL(P(Z|X,\theta^{t+1})||P(Z|X,\theta^t)) \end{align} $$

PS：KL散度，相对熵，其中的负号就是 $\log$ 中的颠倒一下就行~

此外通过 Jensen’s inequality 也可以求证 $$ \log \sum_i p_i f_i \ge \sum_i p_i \log f_i $$ 也可以表示为 $$ \mathbb{E}[\log x] \le \log \mathbb{E}[x] $$

$$ \begin{align} & H(\theta^{t+1},\theta^t) - H(\theta^t, \theta^t) \\
= & \int_Z P(Z|X,\theta^t) \log P(Z|X,\theta^{t+1})dZ - \int_Z P(Z|X,\theta^t) \log P(Z|X,\theta^t)dZ \\
= & \int_Z P(Z|X, \theta^t) \log \frac{P(Z|X,\theta^{t+1})}{P(Z|X,\theta^t)} dZ \\
\le & \log \int_Z P(Z|X,\theta^{t+1})dZ \\
= & \log 1 = 0 \end{align} $$

与大多数非凹函数的优化方法一样，期望最大化算法仅保证收敛到目标函数的局部最大值。使用多个初始启动参数运行过程通常会有所帮助；同样，初始化参数以破坏模型中的对称性也很重要。利用这套有限的技巧，期望最大化算法为数据不完整的模型中的参数估计提供了一个简单而强大的工具。从理论上讲，可以使用其他数值优化技术（例如梯度下降或拟牛顿法）来代替期望最大化。然而，实际上，期望最大化具有简单，健壮和易于实施的优点。

更深层理解

在前面我介绍了$EM$算法的核心的公式的所描述的概念，以及这个迭代过程必将收敛的一个证明，但是我们为什么会得到这个核心公式？或者说，为什么这个公式是合理的？接下来我们通过一些证明过程来看一下，这个公式是否是有意义的~

首先，因为我们是对不完全数据进行求解其最大似然，因此我们可以得到下面这个公式是恒成立的 $$ \log P(X|\theta) = \log \sum_Z P(X,Z|\theta) $$ 直接求解是十分困难的，因此我们对隐变量 $Z$ 引入一个 $q(Z)$ 分布，即假设隐变量可以服从任何的分布情况。

接下来我们将其带入到上述公式中看一下 $$ \begin{align} \log P(X|\theta) & = \log \sum_Z P(X,Z|\theta) \\
& = \sum_Z q(Z) \log P(X|\theta) \\
& = \sum_Z q(Z) \log \frac{P(X|\theta)q(Z)P(X,Z|\theta)}{P(X,Z|\theta)q(Z)} \\
& = \sum_Z q(Z) \log \frac{P(X,Z|\theta)}{q(Z)} + \sum_Z q(Z) \log \frac{P(X|\theta)q(Z)}{P(X,Z|\theta)} \\
& = \sum_Z q(Z) \log \frac{P(X,Z|\theta)}{q(Z)} + \sum_Z q(Z) \log \frac{q(Z)}{P(Z|X, \theta)} \\
& = F(\theta, q(Z)) + KL[q(Z)||p(Z|X,\theta)] \end{align} $$ 这里我们定义了一个函数 $F$ 来代替了上式的前半段，而后半段则是 $KL$ 散度的公式，因为 $KL$ 散度的值肯定是大于等于零的，因此 $F$ 函数则为当前我们求解问题的下界，也被称之为 ELBO（evidence of lower bound）证据下界。

到这一步我们在回头看一下为什么 $EM$ 算法分成了 $E$ 步和 $M$ 步。

首先我们考虑固定 $\theta^t$ 然后来求解 $F$ 在 $q(Z)$ 下的最大值。当 $\log P(X|\theta)$ 的值固定下来时，如果我们想让 $F(\theta^t, q(Z))$ 最大的化，即我们需要使得 $KL$ 的值为0，而 $KL$ 的值仅在 $q(Z) = P(Z|X, \theta^t)$ 的情况下才等于0，所以这就是为什么我们选择了求解 $P(Z|X,\theta^t)$ 来作为 $q(Z)$ 的分布情况，也就是 $E$ 步的得来。

然后我们考虑固定 $q$ 来求解 $\theta$ 下的最大值。在这种情况下，$F(\theta, q(Z)) = Q(\theta, \theta^t)$ ，而这一步就是 $M$ 步的由来。

因此，$EM$ 算法可以看做是 $q$ 和 $\theta$ 上的坐标提升算法，以最大化 $F$ 函数（$\log P(X|\theta)$ 的下界）。