[读书笔记]《西瓜书》第七章 贝叶斯分类器 补充一

第七章 贝叶斯分类器 补充一

整理完了西瓜书中第七章的相关内容之后，发现有一些内容需要进行补充阐述，梳理了一下大致有三个方面的内容：“判定模型”和“生成模型”、EM算法和采样方法总结，感觉一篇博文应该放不下这么多的内容，所以估计是还要分为三篇博文来进行梳理了。此外对于概率图模型的部分内容，这一章其实也涉及了一点内容，但是考虑到后面第十四章有专门的一个概率图模型的章节，这里就不进行展开梳理了，后期再详说~

“判别式模型”和“生成式模型”

在第七章中，西瓜书中，给出了在概率框架的角度下来理解机器学习的时候，其所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率 $P(c|\boldsymbol{x})$ 。然后书中给出了两种策略：“判别式模型”（discriminative models）和“生成式模型”（generative models）。然而本人资质不行，对于西瓜书中表达的内容没法理解的很透彻，所以并没有理解的很透彻这两种模型到底有什么区别~

PS：在看了很多遍相关的内容和相关书籍上的知识点，过了半年回过头来梳理博文的时候发现，自己大概的有那么点感觉了~ 接下来我将结合自己的理解并将相关的一些资料的内容都整理在下面，其中有自己的一些“浅薄”的见解（可能不对，且看且笑~）

直观感受

在网上收集相关知识点的时候，发现维基百科给出的Generative条目里面有个经典的案例，非常的直观，不过在知乎上有人介绍过了，所以这里就不引用原文了，直接摘抄知乎上作者给出的中文例子：

假设有四个samples：

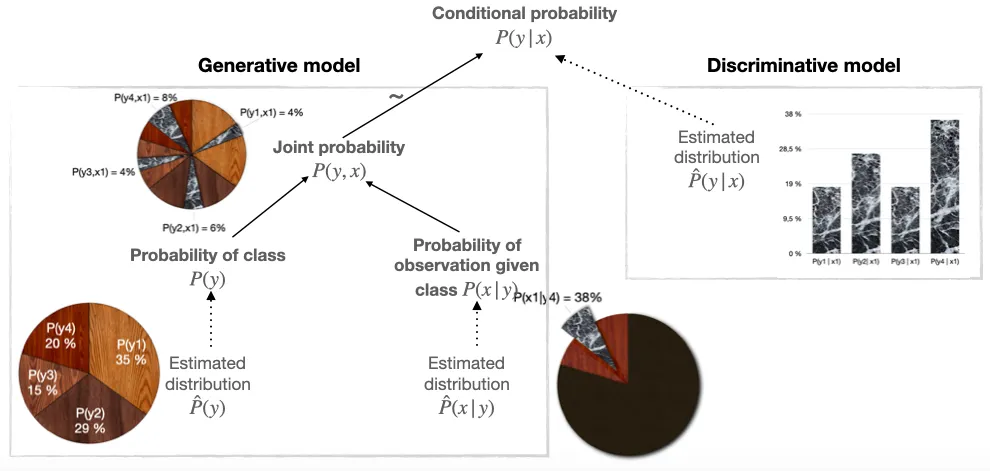
生成式模型的世界是这个样子：

判定式模型的世界是这个样子：

通过上面的例子，给人的直观冲击感是十分强烈的。可以看到，在生成式模型中我们针对的建模对象是 $P(x,y)$ 的联合概率分布，即上图生成式模型中的每个概率值之和是等于1的 $$ \sum P(x, y) = 1​ $$ 而在判别式模型中我们针对的建模对象是 $P(y|x)$ 的后验概率分布，即上图判别式模型中的每个横行的概率值之和是等于1的 $$ \sum_{y} P(y|x) = 1 $$

有了上面的直观感受之后，我们接下来分别来看下到底什么是生成式模型，什么是判别式模型~

PS：在网上找了很多相关的定义，考虑到有人说联合概率有人说先验分布等等的口径，这里就引用了谷歌的机器学习开发者教程中的定义来做标准。

生成式模型

Generative models capture the joint probability $p(X, Y)$, or just $p(X)$ if there are no labels. —— quote from develop.goolge.com

在生成式模型中，一开始建模时候的视角是就是聚焦在数据集本身的分布上面的，然后通过此来告诉使用者，你给出的数据在建模后的数据集分布中处在一个什么样的位置。

在网上无论是说后验分布的求得是基于先验分布还是说基于联合分布之类的其实本质上结合贝叶斯定理公式来看都是一样。 $$ P(c|\boldsymbol{x}) = \frac{P(\boldsymbol{x}, c)}{P(\boldsymbol{x})} = \frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})} $$

前者可以看做是基于联合分布结合数据分布求得后验分布，后者可以看做是基于先验分布和类条件分布结合数据分布求得后验分布，其实本质上都一样~

配合上面👆wikipeida给出的例子，应该直接就一目了然了，即生成式模型关心的是数据集的在整个空间中的分布情况，如果有标签，则看标签和数据的联合分布，如果没有标签则只关注数据集的分布即可~

判别式模型

Discriminative models capture the conditional probability $p(Y | X)$. —— quote from develop.goolge.com

在判别式模型中，建模的视角只聚焦在数据到底属于哪个标签，即其忽略了样本数据到底是什么的一个状态，只关注于其属于哪个类别。

因此我们可以直观的感受到判别式模型相对于生成式模型来说，其忽略了样本本身的分布情况，所以在建立模型的过程当中，其相对于生成式模型要更精炼一些~

配合上面👆wikipeida给出的例子，也同样很好理解，即我们只关注 $x=0$ 的时候其到底有多大的概率属于哪个标签，而并不关注 $x$ 本身有多大的概率属于 0 或者 1。

PS：在这里就要引入一下个人的浅薄的见解了，当然不一定对。个人理解其实这里在任何书里都是使用了“概率”一词，感觉自己在理解过程中的时候究其原因就是这个词的使用，其实这个源自于英文版的文章中的翻译。相对的，我觉得如果将其看做是置信度可能会跟容易跟生成式模型区分开，即在类别中，当前数据在每个类别的置信度是多少。当然直观的看来置信度之和肯定不是一，但是相对于概率来说，将其理解成各类别置信度之和为一的这个角度来看待的话，可能对于自己来说更好理解~

两者对别

在网络上的例子中，下面是最常见的一幅图片

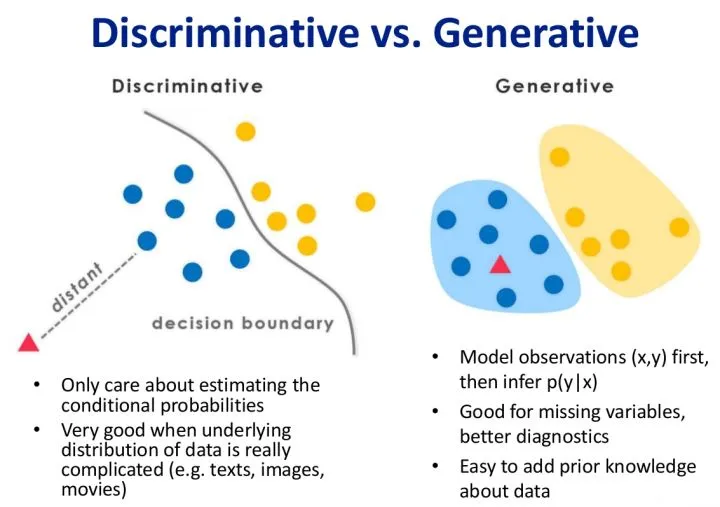
这里本人也就不多阐述了，因为知乎上的大佬已经解释的很完备了，我将其解释的内容直接引用在此：

对于判别式模型来说求得 $P(Y|X)$，对未见示例 $X$ ，根据 $P(Y|X)$ 可以求得标记 $Y$ ，即可以直接判别出来，如上图的左边所示，实际是就是直接得到了判别边界，所以传统的、耳熟能详的机器学习算法如线性回归模型、**支持向量机(SVM)**等都是判别式模型，这些模型的特点都是输入属性 $X$ 可以直接得到 $Y$（对于二分类任务来说，实际得到一个 score，当 score 大于 threshold 时则为正类，否则为反类）

（根本原因个人认为是对于某示例 $X_1$ ，对正例和反例的标记的条件概率之和等于1，即 $P(Y_1|X_1)+P(Y_2|X_1)=1$）

而生成式模型求得 $P(Y,X)$，对于未见示例 $X$，你要求出 $X$ 与不同标记之间的联合概率分布，然后大的获胜，如上图右边所示，并没有什么边界存在，对于未见示例（红三角），求两个联合概率分布（有两个类），比较一下，取那个大的。机器学习中朴素贝叶斯模型、**隐马尔可夫模型(HMM)**等都是生成式模型，熟悉Naive Bayes的都知道，对于输入 $X$ ，需要求出好几个联合概率，然后较大的那个就是预测结果

（根本原因个人认为是对于某示例 $X_1$，对正例和反例的标记的联合概率不等于1，即$P(Y_1,X_1)+P(Y_2,X_1)<1$，要遍历所有的 $X$ 和 $Y$ 的联合概率求和，即$sum(P(X,Y))=1$，具体可参见楼上woodyhui提到的维基百科Generative model里的例子）

但是这个解释的作者给出的例子感觉就相对有一些模糊不清了，所以这里不做引用，而使用谷歌的在对其进行解释时给出的例子~

PS：此外CRF模型为判别式模型，而HMM为生成式模型

Discriminative and generative models of handwritten digits

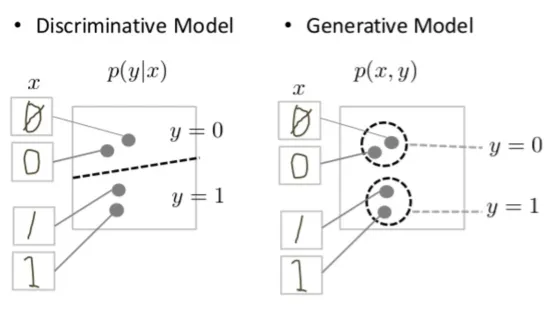
The discriminative model tries to tell the difference between handwritten 0’s and 1’s by drawing a line in the data space. If it gets the line right, it can distinguish 0’s from 1’s without ever having to model exactly where the instances are placed in the data space on either side of the line.

In contrast, the generative model tries to produce convincing 1’s and 0’s by generating digits that fall close to their real counterparts in the data space. It has to model the distribution throughout the data space.

判别模型试图通过在数据空间中画一条线来分辨手写0和1之间的区别。 如果正确，则可以不必在行两边的数据空间中准确建模实例的位置，就可以将0与1区分。

相反，生成模型试图通过产生接近数据空间中真实对数的数字来产生令人信服的1和0。 它必须对整个数据空间的分布进行建模。

—— quote from Background: What is a Generative Model

各自的特点

PS：特点这块李老师的《统计学习方法》中做了罗列，整理如下~

生成式方法的特点

生成式方法可以还原出联合概率分布 $P(X，Y)$ ，而判别方法则不能；生成式方法的学习收敛速度更快，即当样本容量增加的时候，学到的模型可以更快地收敛于真实模型；当存在隐变量时，仍可以用生成方法学习，此时判别方法就不能使用了。

PS：尤其重要的一个模型——高斯混合模型 （GMM）后面会提到~

判别式方法的特点

判别方法直接学习的是条件概率 $P(Y|X)$ 或决策函数 $f(X)$，直接面对预测，往往学的准确率更高；由于直接学习 $P(Y|X)$ 或 $f(X)$，可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习任务。

Reference

• 《机器学习》周志华
• 《统计机器学习》李航
• Background: What is a Generative Model?
• 机器学习“判定模型”和“生成模型”有什么区别？ - politer的回答 - 知乎
• 机器学习“判定模型”和“生成模型”有什么区别？ - woodyhui的回答 - 知乎
• Introduction to generative and discriminative models
• Generative vs. Discriminative Models in Machine Learning
• Generative vs. discriminative