[读书笔记]《西瓜书》第六章 支持向量机 补充
![[读书笔记]《西瓜书》第六章 支持向量机 补充](/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_900x500_fit_q75_box.jpg)
第六章 支持向量机 补充
SVM这一章节其实在西瓜书中已经介绍的相当完整了,而且在各大网络上的教程中,也是介绍的相对比较详细的那一章节。不过个人理解,其实核技巧或者说核函数并不一定用在SVM中,而且在后面的章节中也出现过。不过,相对于支持向量机的本身的理解来说,核技巧相对来说要难理解的多一些。
核技巧
其实核技巧是一个本身非常纯粹的数学方法而已,而且是一种比较投机取巧的方法,目的其实就是为了减少计算的工作量。如果想从根本上理解这个方法,就要先理解一下核技巧出现的问题前提。
问题描述
假设现在我们手中有两个向量,现在我们的目标是要计算着两个向量的点积,即我们可以设用数学的公式表达的话为如下形式 $$ T: <\boldsymbol{x}, \boldsymbol{y}> $$ 如果这两个向量 $\boldsymbol{x}$ 和 $\boldsymbol{y}$ 是我们熟悉的比如二维向量的话,那么计算起来就非常的简单,即我们对位相乘再相加就行了。但是现在我们不止于此,我们再推广一下,假设现在这两个向量都是一万维的向量呢?即我们需要计算的工作量变成了 $$ T:<\boldsymbol{x},\boldsymbol{y}> = 10000次乘法 + 10000次加法 $$ 这时候这个计算的复杂度已经很高了,也就是说要计算这个结果就已经是非常困难的(当然在如今来看这个计算复杂度并不高)。我们再继续推广一下,假设现在我们不仅是要计算两个一万维的向量,而是要计算其在进行某种非线性变换后的得到的两个向量的内积呢?即我们定义非线性变换为 $\Phi: \boldsymbol{x} \mapsto \phi(\boldsymbol{x}) $ ,然后我们得到的是目标公式是 $$ T:< \phi(\boldsymbol{x}), \phi(\boldsymbol{y})> = 10000次乘法 + 10000次加法 $$
PS:为了方便说明,这里不考虑非线性变换后导致的特征维度变化的情况。
上面的这个目标公式里还没加上非线性变换函数的计算量,这样,我们假设一下,非线性函数仅仅由每个向量内部的两个相邻特征相乘得到,于是我们又可以的得到 $$ T:<\phi(\boldsymbol{x}), \phi(\boldsymbol{y})> = 10000次乘法 + 10000次加法 + 20000次乘法(非线性) $$ 怎么样,看似计算量还可以是不是,但是其实本身上复杂度已经很高了,另外考虑到实际的应用场景来说,我们有一个比较难以抉择的问题,即这个非线性变换如何选择?究竟哪个非线性变换才比较适合?虽然我们现在选择的是两个相邻的特征两两相乘,但是如果是两两相加的和的平方更好呢?
OK,那么再接着推广,如果现在不是计算两个向量呢?而是计算一个包含10000个向量的矩阵呢?即我们现在要做这10000个向量的两两之间的内积,那么这个时候运算量可就海了去了~
于是,英明神武的数学家开始考虑如何偷懒,即:如果我们并不用选取任何的非线性变换函数呢?而是仅仅找到一个函数使得我们可以直接得到这两个向量在我们理想问题中的答案呢?
用西瓜书中的话来说:能不能在原始空间中找到一个函数 $K(x_i, x_j)$ 使得 $K(x_i, x_j) =<\phi(x_i), \phi(x_j)>$ 呢?用在我们当前这个情况就是,能否直接找到一个函数将原来两个向量直接带入进去,直接求得我们的解,即 $$ T:<\phi(\boldsymbol{x}), \phi(\boldsymbol{y})> = K(\boldsymbol{x}, \boldsymbol{y}) $$
PS:什么是内积空间呢?
内积空间是数学中的线性代数里的基本概念,是增添了一个额外的结构的向量空间。这个额外的结构叫做**内积**或标量积。内积将一对向量与一个标量连接起来,允许我们严格地谈论向量的“夹角”和“长度”,并进一步谈论向量的正交性。内积空间由欧几里得空间抽象而来(内积是点积的抽象),这是泛函分析讨论的课题。
内积空间有时也叫做准希尔伯特空间(pre-Hilbert space),因为由内积定义的距离完备化之后就会得到一个希尔伯特空间。 — quote by wikipedia
最终我们通过这种技巧得到的就是,我们不需要将原始向量先进行非线性变换,而是直接通过一个函数求得其变换后得到的内积,最终数学家们定义这种简化计算的方法称之为核技巧(The Kernel Trick),而这个函数就称之为核函数(Kernel Function)。
SVM使用
首先要声明的就是核函数不一定仅仅在SVM中使用,在其他模型中也可以使用,只是在西瓜书的章节安排中,第一次接触是在SVM中。另外就是要特别声明一下的是,在SVM中使用核技巧是存在理论前提的。
Cover’s theorem is a statement in computational learning theory and is one of the primary theoretical motivations for the use of non-linear kernel methods in machine learning applications. The theorem states that given a set of training data that is not linearly separable, one can with high probability transform it into a training set that is linearly separable by projecting it into a higher-dimensional space via some non-linear transformation. The theorem is named after the information theorist Thomas M. Cover who stated it in 1965. In his own words,
A complex pattern-classification problem, cast in a high-dimensional space nonlinearly, is more likely to be linearly separable than in a low-dimensional space, provided that the space is not densely populated.
— Cover, T.M., Geometrical and Statistical properties of systems of linear inequalities with applications in pattern recognition, 1965
— quota by wikipedia
Cover’s theorem是计算学习理论中的一个基石,是在机器学习应用程序中使用非线性核方法的主要理论动机之一。 该定理指出,给定一组不可线性分离的训练数据,可以通过一些非线性变换将其投影到更高维的空间中,从而很有可能将其转换为可线性分离的训练集。 该定理以信息理论家Thomas M. Cover于1965年提出的名字命名。
PS:虽然我们经常在一些实验中直接使用SVM来进行分类,但是很少注意使用的前提。这里我觉得还是需要注意一下的。
常见的核函数
线性核
$$ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \boldsymbol{x}_i^{\top}\boldsymbol{x}_j + c $$
PS:这里其实看完之后存在一个问题,即为什么会存在线性核?看起来只是增加了一个常数而已。
在查阅了一些资料之后,发现线性核是将原始的特征空间进行扩张,然后构建了一个同构的特征空间,预期结果是将原始特征空间分隔的更加清晰与明显,而这个时候,就可以感受到,在这样的空间中,我们得到结果仍然是无法解决异或问题的。
此外在stackoverflow网站上找到了一个问题也是关于线性核如何使用的,其结论基本和吴恩达老师的视频中说到的是一致的。
One more thing to add: linear SVM is less prone to overfitting than non-linear. And you need to decide which kernel to choose based on your situation: if your number of features is really large compared to the training sample, just use linear kernel; if your number of features is small, but the training sample is large, you may also need linear kernel but try to add more features; if your feature number is small (10^0 - 10^3), and the sample number is intermediate (10^1 - 10^4), use Gaussian kernel will be better.
As far as I know, SVM with linear kernel is usually comparable with logistic regression .
— quota by https://stackoverflow.com/questions/20566869/where-is-it-best-to-use-svm-with-linear-kernel
简单来说:最简单,最安全,最不容易过拟合
多项式核
$$ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = (\alpha \boldsymbol{x}_i^{\top}\boldsymbol{x}_j + c)^d $$
相比于线性核为什么会存在来说,多项式核就更加的容易理解了,即为了将不可以线性可分的数据进行分类的时候,我们可以进行将期望求得的超平面转化成曲面来看待。
因此如何选择degree在多项式核中更为重要,因为这时借助背景知识我们可以设置所期望的特征之间的关系次方,这是十分重要的,因为到这时我们还可以对最终的结果产生一个解释和预期。
高斯核
$$ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j) = \exp(-\alpha\Vert\boldsymbol{x}_i - \boldsymbol{x}_j\Vert^2) $$
高斯核也称为径向基核,即,当我们的 $\alpha$ 并非随机选取的时候,而是基于高斯分布的公式得到时,这时径向基&就变成了高斯核。
对比线性核和多项式核来说,高斯核的特别之处就是其可以映射到无穷维的特征空间。
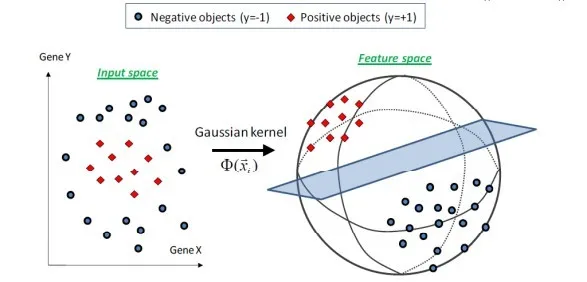
优点:
- 可以映射到无限维
- 决策边界更为多样
- 只有一个参数,相比多项式核容易选择
缺点:
- 可解释性差(无限多维的转换,无法算w)
- 计算速度比较慢(解一个对偶问题)
- 容易过拟合(参数选不好时容易overfitting)
Sigmoid核
采用Sigmoid函数作为核函数时,支持向量机实现的就是一种多层感知器神经网络,应用SVM方法,隐含层节点数目(它确定神经网络的结构)、隐含层节点对输入节点的权值都是在设计(训练)的过程中自动确定的。而且支持向量机的理论基础决定了它最终求得的是全局最优值而不是局部最小值,也保证了它对于未知样本的良好泛化能力而不会出现过拟合现象。
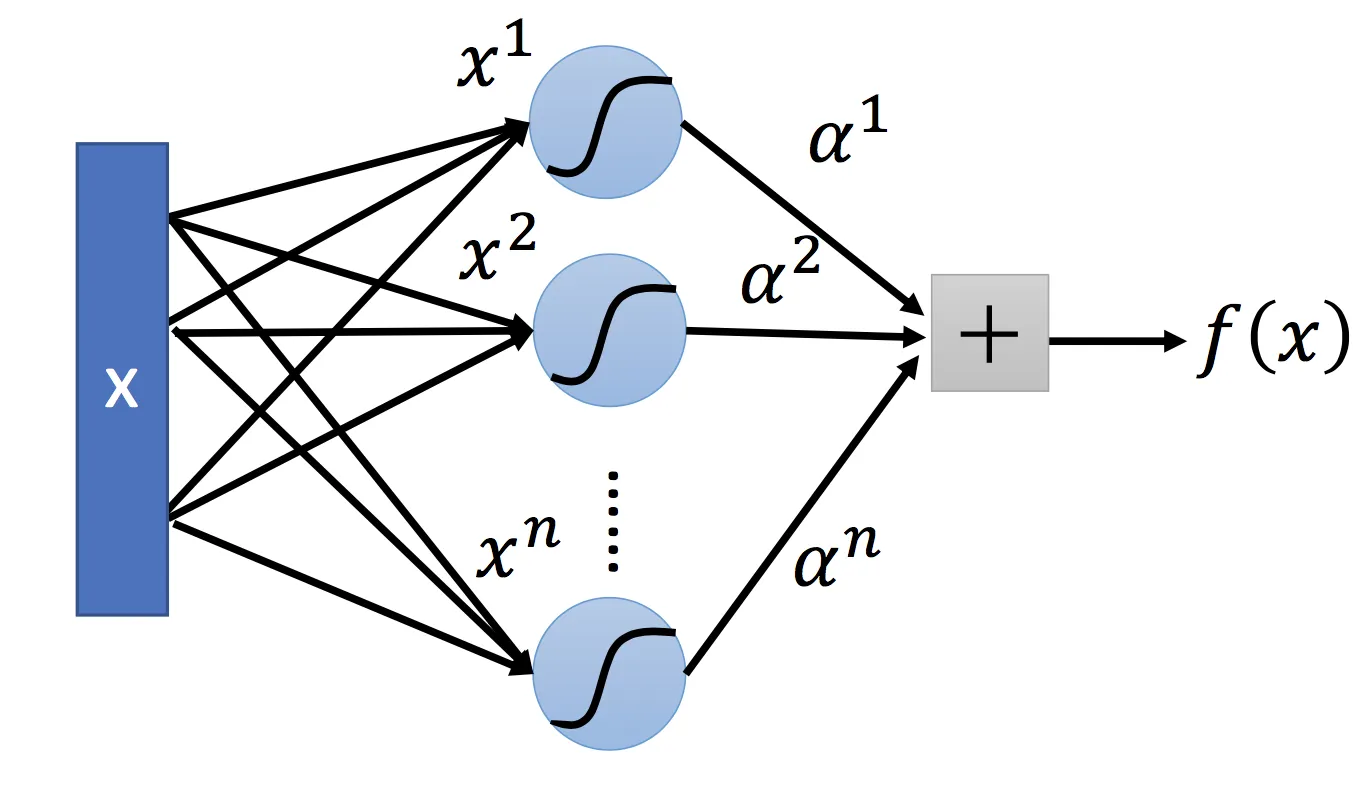
PS:我记得当初在那里看到过,SVM的作者就人为,神经网络模型只不过是SVM的拓展而已,但是写文章的时候没找到。
![[读书笔记]《西瓜书》第六章 支持向量机](https://cdn.jsdelivr.net/gh/Ryuchen/ryuchen.github.io@master/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_700x350_resize_q75_box.jpg)