[读书笔记]《西瓜书》第五章 神经网络 补充六

第五章 神经网络 补充六

神经网络是现在主流的机器学习处理问题的手段，因此需要更加细致的去学习，所以这里自己搜集了一些补充知识点，而且感觉应该需要拆分成几个小章节进行论述，因此这里会使用副标题

Why Deep?

PS：终于迎来的神经网络章节补充的最后一篇博文了，这个篇博文主要是为了将前面的补充内容进行一个汇总，算是很好的给这一章节进行收尾了。题目的标题选定就是李宏毅老师的视频课程的一个章节的标题，我觉得对于整个神经网络知识的内容进行了言简意赅的概括。

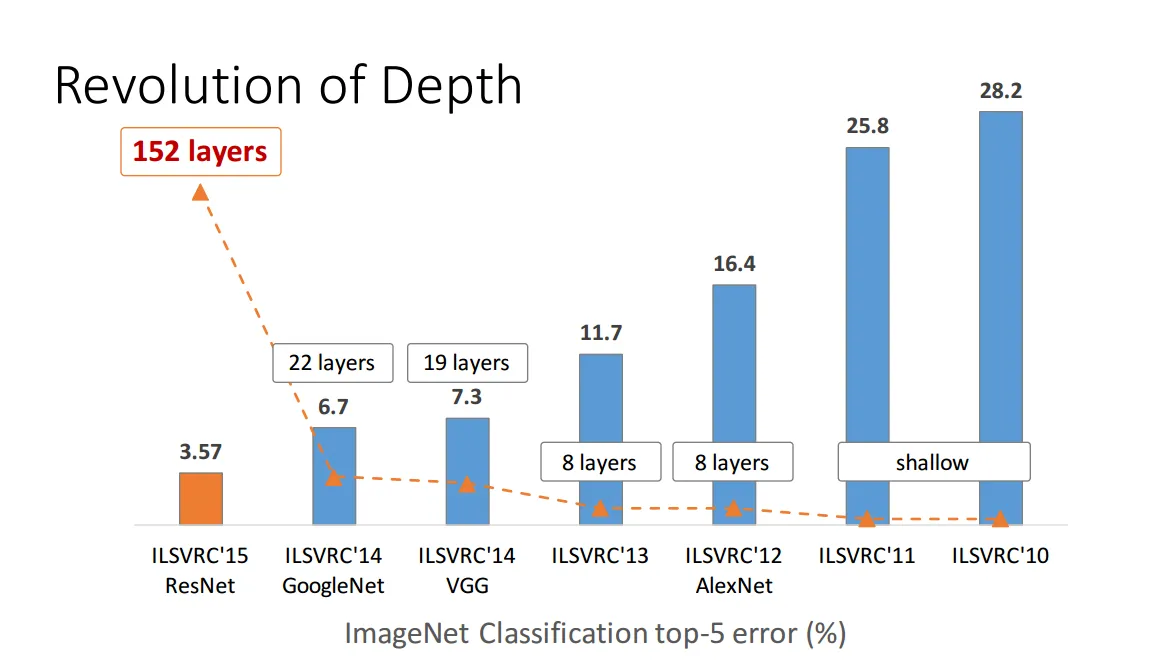
首先让我们从一个普遍认识开始：深度神经网络就是简单前馈神经网络叠加了多个隐层。为了对这个论调进行证伪，我们需要逐渐的将之前的补充的内容进行串联起来。但是就算是将之前的博文补充的内容全部加起来也不能够完全阐释这个问题，更加具体的内容还需要其他的一些知识进行补充，但是我们也能够对这个论调的确切有一些比较全面的认识了。

学习能力从哪来？

通过本章节第一篇补充博文的内容中，整理了感知机模型相关的知识。了解了感知机模型无法解决异或问题之后，我们借助章节第二篇补充博文知道多层感知机，即神经网络模型能够解决异或问题之后，那么我们需要确定的一点是之所以能够解决异或问题，与之对应的学习能力究竟从哪里得到的？

当然有了一定的基础的逻辑运算知识之后，我们可以知道神经网络模型的学习能力源自线性函数与非线性函数相互叠加得到的。因为从数学角度来看待现实中处理的问题的时候，我们可以对其进行一个基本的假设，即我们可以使用一个足够复杂的函数来拟合任意一个问题的求解函数。而这个函数的关键难点是，我们无法得知需要使用什么样的组合方式才能得到这样的一个函数。但是借助数学上的一些基本函数的组合，我们可以拟合任意函数图像的这样一个特性。自然我们可以通过一种网状结构将线性函数和非线性函数进行组合得到一些更为复杂的函数，即我们可以借助神经网络模型的结构，将线性函数和非线性函数交替组合在一起以求得拟合任何现实问题中的求解函数。

PS：当然相比于传统的VC维问题的证明来看，我们目前还没法证明，一个神经网络模型的求解问题也存在VC Bound，但是就目前看到的效果来说，我们可以这么做，难点只是我们无法得知具体需要如何的网络模型和神经元的数量。

通用逼近定理（Universal Approximation Theorem）

PS：上面的解释只是我个人在记忆过程中的通俗理解，而通用逼近定理（Universal Approximation Theorem）则是这个问题的确切解答

从数学上讲，任何神经网络体系结构都旨在寻找可以将属性 $x$ 映射到输出 $y$ 的任何数学函数 $y = f(x)$。 此功能（即映射）的准确性取决于数据集的分布和所用网络的体系结构而有所不同。 函数 $f(x)$ 可以任意复杂。 通用逼近定理告诉我们，神经网络具有某种通用性，即无论 $f(x)$ 是什么，都有一个网络可以近似地逼近结果并完成工作！ 该结果适用于任意数量的输入和输出。

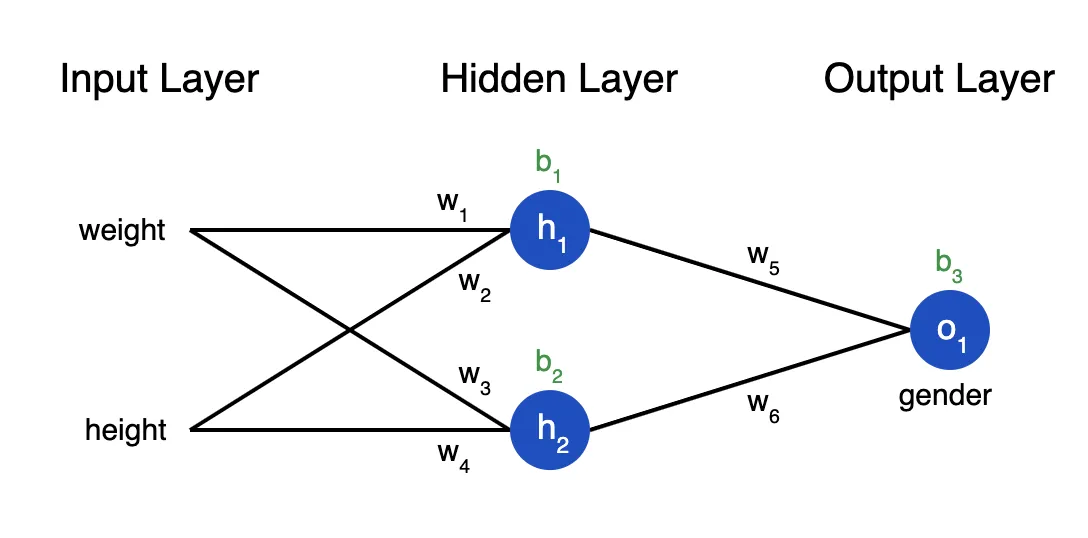
为什么不使用机器学习模型？

在传统机器学习的模型中，我们都有一个理论基石，即VC维。也就是说随着数据量的增多，我们问题的求解可能会变成一个相对平稳的状态，也就是说我们模型的效果并不会因为大数量的堆砌而变得效果更佳的好，而是在一定的时候趋向于饱和。但是神经网络似乎并不具有这样的现象，因为随着众多的实验或实践现象标明，几乎我们给神经网络模型的数据量越多，那么我们得到的模型效果反而会更好。

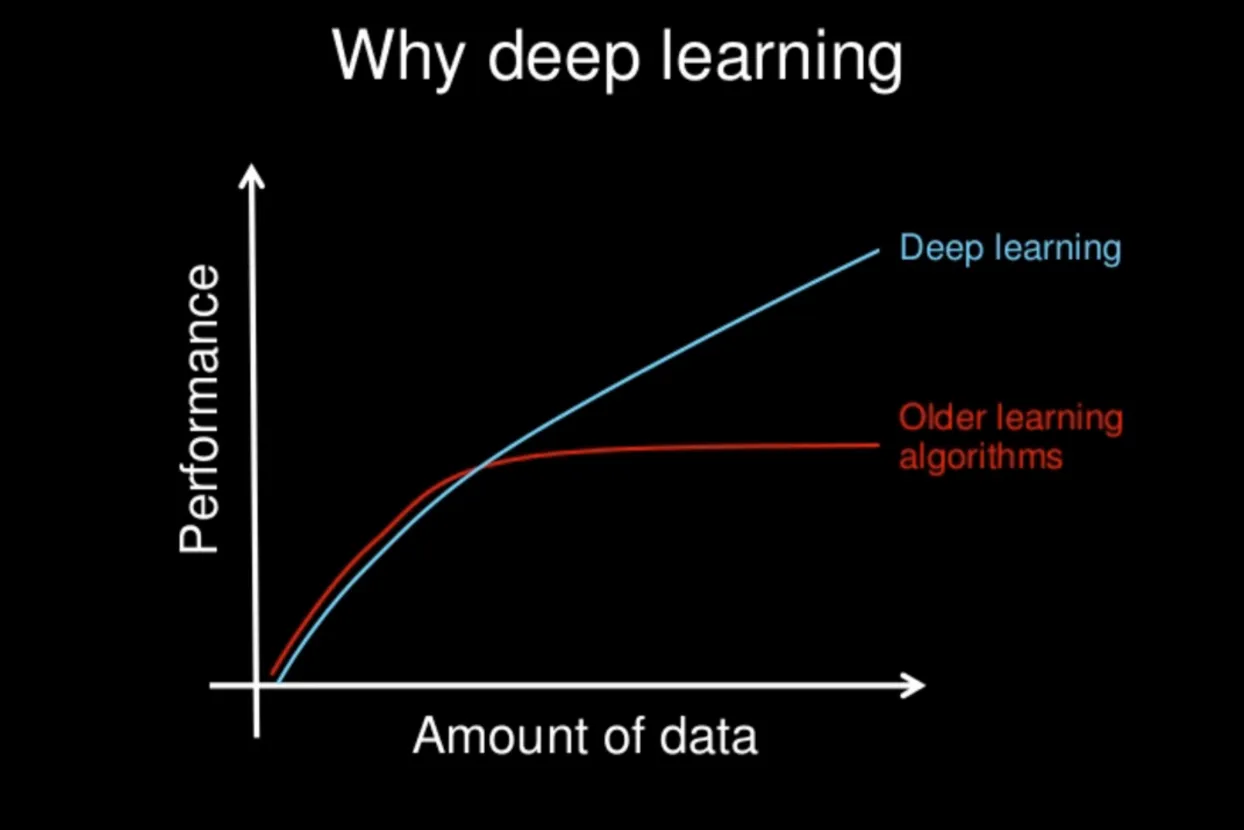
而学术界，也缺失在找一个类似VC维的理论，为这一现象进行支撑或者说证明。 但并不妨碍如今，随着易于访问的有益计算环境的出现，实时实验和改进算法和体系结构变得更加容易，因此在短时间内就产生了越来越好的实践。 深度神经网络已在许多领域中找到了广泛的应用，例如计算机视觉，自然语言处理，推荐系统等等，并且做到了非常好的实践效果。

更宽还是更深？

既然深度神经网络模型这么优秀，那么我们应该选择更深的结构还是更宽的结构呢？

首先，借助上面的原则来看，我们根本没有理由需要深层结构的神经网络：给定足够的训练数据，只有一个隐藏层的足够宽的神经网络可以近似任何（合理的）函数。

那么我们为什么还要深层的网络结构呢？

首先，及其宽泛的神经网络太过优秀，就像一个超级无敌的”书呆子“一样，这些非常宽泛的浅层网络非常擅长记忆，但不那么容易泛化。因此，如果用所有可能的输入值训练网络，那么超宽网络最终会记住你想要的相应输出值。但这没有用，因为对于任何实际的应用程序，你都不会掌握所有可能的输入值。还记得我们在上一篇博文中提到的那个理论吗？神经网络模型一定是过拟合的，而正是因为此我们不需要特别宽的神经网络来对我们的数据集进行训练。

其次是，多层次的结构设计的优点是它们可以学习各种抽象级别的功能。例如，如果你训练一个深度卷积神经网络对图像进行分类，你会发现第一层将训练自己以识别非常基本的事物（例如边缘），而第二层将训练自身以识别边缘的集合（例如形状），下一层将训练自己以识别诸如眼睛或鼻子等形状的集合，而下一层将学习甚至更高阶的特征（如脸部）。多层在概括方面要好得多，因为它们学习原始数据和高级分类之间的所有中间特征。

总结一下，即我们可以这么来：从神经网络模型的同层的截面来看的话，同一层次中的神经元之间是一种module ensemble的方式，即将不同的学习模块组合在了一起，每个神经元学习不同的内容；而从层级的截面看这个问题的话，不同层次之间的神经元是一种feature ensemble的方式，即将不同的层级特征组合在了一起，每个层次的神经元学到的特征层次不同；最后从整体结构的截面看这个问题的话，整个神经网络模型是一种model ensemble的方式，即神经网络模型可以看做将多个网络结构的神经网络模型通过参数共享和神经元共享的方式组合在一起。

因此，这说明了为什么你可能会使用深层网络而不是非常宽泛但浅薄的网络。但是，为什么不建立一个非常广泛的网络呢？我认为答案是，你希望你所训练的网络模型结构尽可能小并且能够产生良好的结果。随着网络规模的增加，实际上只是在引入网络需要学习的参数，从而增加了过度拟合的机会。如果你构建了一个非常广泛，非常深入的网络，则每层都有机会记住你要的输出内容，最终你将得到一个无法泛化的神经网络。

Reference

• Do Deep Nets Really Need to be Deep?

• Wide & Deep Learning: Better Together with TensorFlow

• What is the difference between a neural network and a deep neural network, and why do the deep ones work better?

• Neural Networks and the Universal Approximation Theorem