[读书笔记]《西瓜书》第五章 神经网络 补充四
![[读书笔记]《西瓜书》第五章 神经网络 补充四](/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_900x500_fit_q75_box.jpg)
第五章 神经网络 补充四
神经网络是现在主流的机器学习处理问题的手段,因此需要更加细致的去学习,所以这里自己搜集了一些补充知识点,而且感觉应该需要拆分成几个小章节进行论述,因此这里会使用副标题
反向传播算法
PS: 这里本来想是进行整理一下的,自己学习过程中网上搜集的资料的,但是奈何大多数博文都是一大堆公式,看的人索然无味,但在自己准备着手开始自己写的时候,发现了一篇好文,简单清晰明了,没有一大堆的公式,于是翻译在此。
原文链接: Backpropagation
介绍
Backpropagation is an algorithm that calculate the partial derivative of every node on your model (ex: Convnet, Neural network). Those partial derivatives are going to be used during the training phase of your model, where a loss function states how much far your are from the correct result. This error is propagated backward from the model output back to it’s first layers. The backpropagation is more easily implemented if you structure your model as a computational graph.
反向传播是一种计算机器学习模型(例如:Convnet,神经网络)中每个节点的偏导数的算法。这些偏导数将会在你训练模型的阶段中使用,当你的损失函数告诉你,你的模型结果现在距离真实值有多远时。这里的误差将会通过反向传播算法通过模型输出层一直传回第一层。在使用过程中,如果你的模型能够构造成计算图,那么反向传播算法的使用将会十分容易。
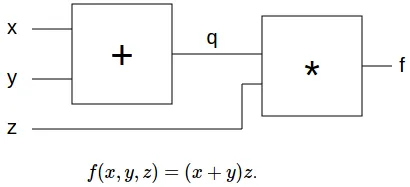
The most important thing to have in mind here is how to calculate the forward propagation of each block and it’s gradient. Actually most of the deep learning libraries code is about implementing those gates forward/backward code.
这里要记住的最重要的事情是如何计算每个块的前向传播及其梯度。实际上大多数深度学习的库都已经实现了前向传播和后向传播的功能。
基本单元
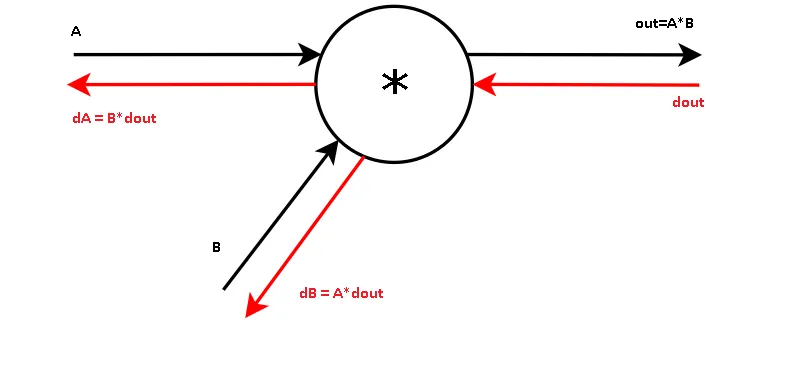
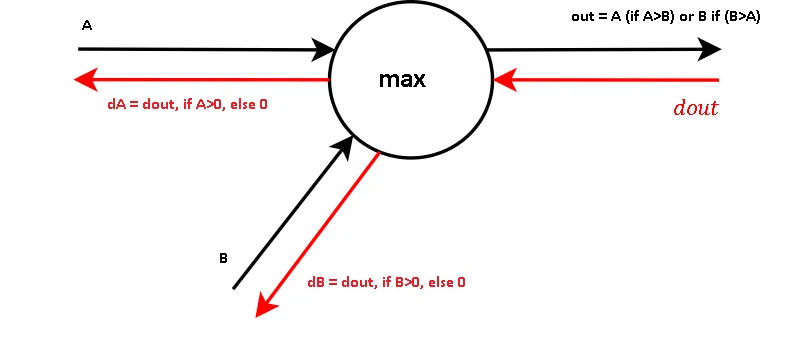
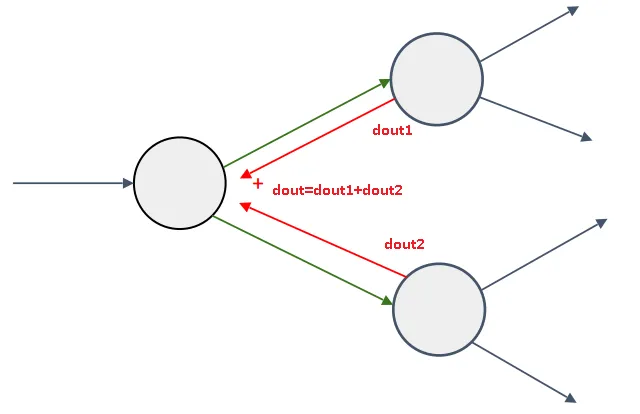
Some examples of basic blocks are, add, multiply, exp, max. All we need to do is observe their forward and backward calculation
基本块的一些示例是加,乘,乘,最大值。我们要做的就是观察它们的前向传播和后向传播的计算过程。

Some other derivatives:
一些其他的导数公式:
$$f(x) = \frac{1}{x} \quad \rightarrow \quad \frac{df}{dx} = - \frac{1}{x^2} $$
$$f_c(x) = c + x \quad \rightarrow \quad \frac{df}{dx} = 1$$
$$f(x) = e^x \quad \rightarrow \quad \frac{df}{dx} = e^x$$
$$f_a(x) = ax \quad \rightarrow \quad \frac{df}{dx} = a$$
Observe that we output 2 gradients because we have 2 inputs… Also observe that we need to save (cache) on memory the previous inputs.
观察到这里我们输出了2个梯度值,是因为我们有2个输入… 还观察到我们需要将先前的输入保存(缓存)在内存中。
链式法则
Imagine that you have an output $y$, that is function of $g$, which is function of $f$, which is function of $x$. If you want to know how much $g$ will change with a small change on $dx(\frac{dg}{dx})$, we use the chain rule. Chain rule is a formula for computing the derivative of the composition of two or more functions.
想象一下,您有一个输出 $y$,它是 $g$ 的函数输出,而 $g$ 又是 $f$ 的函数,$f$ 又是 $x$ 的函数。 如果您想知道 $g$ 随 $dx(\frac{dg}{dx})$ 的微小变化而变化多少,我们使用链式规则。 链规则是用于计算两个或多个函数组成的导数的公式。
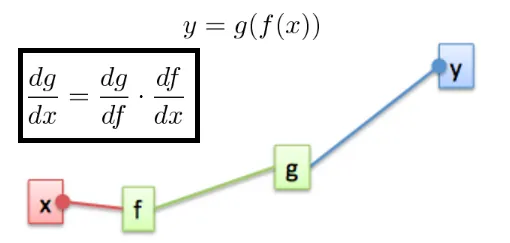
The chain rule is the work horse of back-propagation, so it’s important to understand it now. On the picture bellow we get a node $f(x,y)$ that compute some function with two inputs $x$ , $y$ and output $z$. Now on the right side, we have this same node receiving from somewhere (loss function) a gradient $dL/dz$ which means. “How much $L$ will change with a small change on $z$”. As the node has 2 inputs it will have 2 gradients. One showing how $L$ will a small change $dx$ and the other showing how $L$ will change with a small change $dz$
链式规则是反向传播的工作原理,因此现在了解它非常重要。 在下面的图片中,我们得到一个节点 $f(x,y)$,该节点的函数用两个输入 $x$,$y$ 和输出 $z$ 计算。现在在右侧,该同一个节点从某处(损失函数)接收梯度 $dL/dz$ ,这意味着 “随着 $z$ 的微小变化,$L$ 会变化多少”。 由于节点具有2个输入,因此它将具有 $2$ 个梯度。一个显示 $L$ 如何随着 $dx$ 的小变化而变化,另一个显示 $L$ 如何随着 $dz$ 的小变化而变化
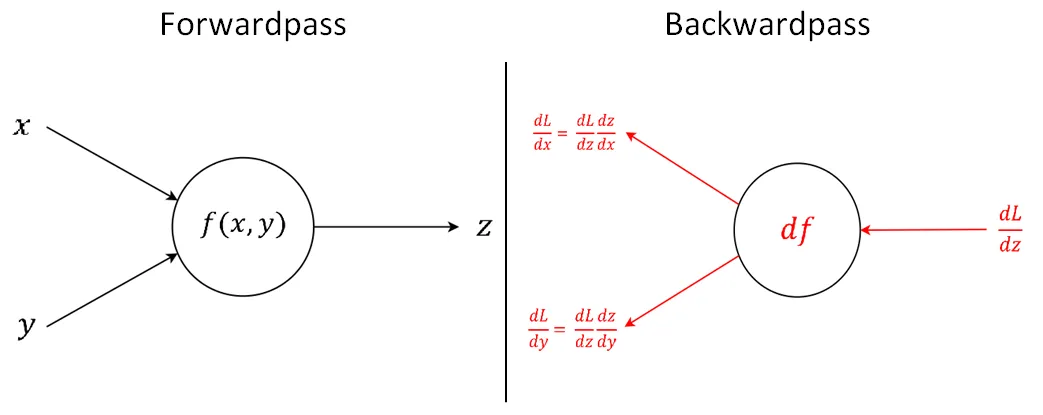
In order to calculate the gradients we need the input $dL/dz$ ($dout$), and the derivative of the function $f(x,y)$, at that particular input, then we just multiply them. Also we need the previous cached input, saved during forward propagation.
为了计算梯度,则我们需要计算 $dL/dz$ 的输入 和 $f(x, y)$ 的导数,并将其进行相乘,另外我们需要在前向传播的过程中在缓存中保存的输入。
计算实现
Observe bellow the implementation of the multiply and add gate on python
下面是乘法和加法的python实现
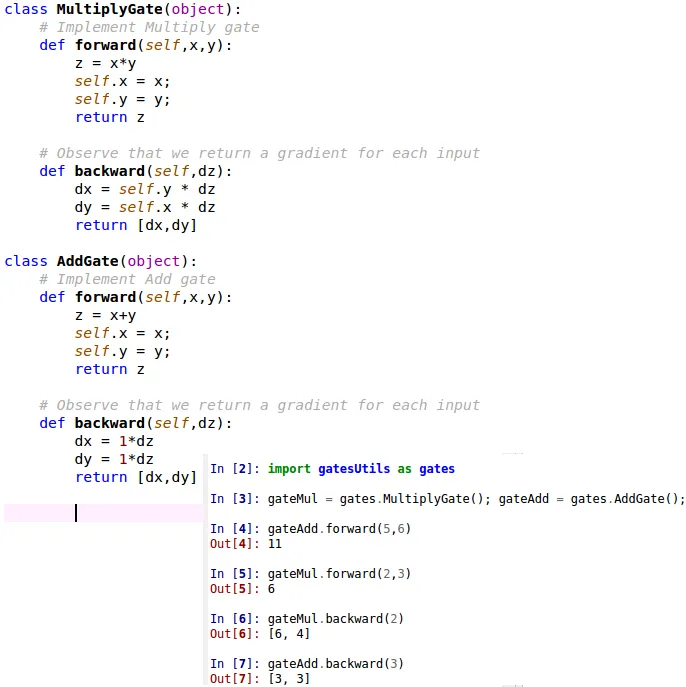
分布计算示例
With what we learn so far, let’s calculate the partial derivatives of some graphs.
通过到目前为止的学习,我们来计算一些图的偏导数。
简单的例子
Here we have a graph for the function $f(x,y,z) = (x+y)*z$
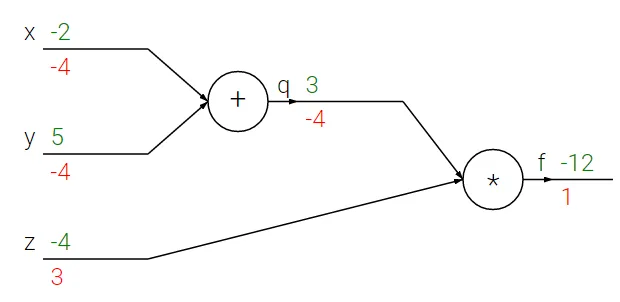
- Start from output node $f$, and consider that the gradient of $f$ related to some criteria is $1$.
- $dq=(dout(1) *z)$, which is -4 (How the output will change with a change in $q$
- $dz=(dout(1)* q)$, which is 3 (How the output will change with a change in $z$
- The sum gate distribute it’s input gradients, so $dx=-4$, $dy=-4$ (How the output will change with $x$, $z$)
图示很清楚就不翻译了~
拥有两个输入的感知机
This following graph represent the forward propagation of a simple 2 inputs, neural network with one output layer with sigmoid activation.
下图表示一个简单的2输入神经网络的向前传播,该神经网络具有一个具有Sigmoid型激活函数的输出层。
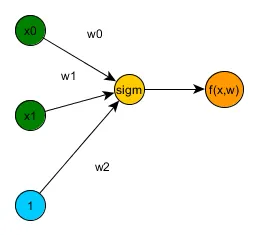
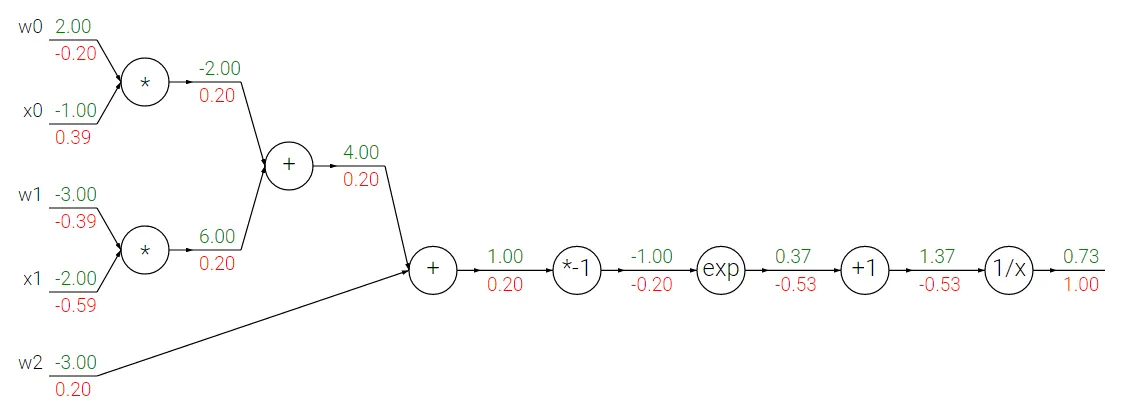
- Start from the output node, considering that or error($dout$) is $1$
- The gradient of the input of the $1/x$ will be $-1/(1.37^2)$, $-0.53$
- The increment node does not change the gradient on it’s input, so it will be $(-0.53 * 1)$, $-0.53$
- The exp node input gradient will be $(\exp(-1(\text{cached input})) * -0.53)$, $-0.2$
- The negative gain node will be it’s input gradient $(-1 * -0.2)$, $0.2$
- The sum node will distribute the gradients, so, $dw2=0.2$, and the sum node also $0.2$
- The sum node again distribute the gradients so again $0.2$
- $dw0$ will be $(0.2 * -1)$, $-0.2$
- $dx0$ will be $(0.2 * 2)$ , $0.4$
梯度消失与梯度爆炸
PS: 这里是补充的额外内容了~
梯度消失问题和梯度爆炸问题一般随着网络层数的增加会变得越来越明显。
PS: 这个注意下,梯度消失与梯度爆炸问题都是在反向传播的过程中,即从后向前传导的过程中出现的问题
梯度消失(gradient vanishing problem)
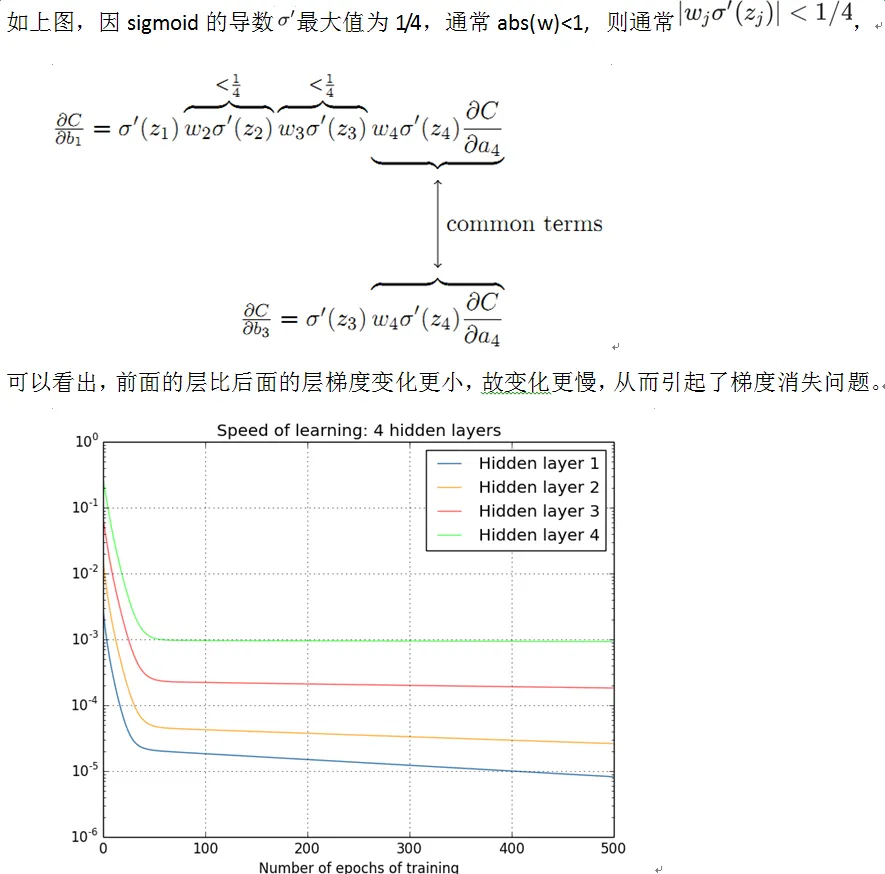
梯度爆炸(gradient exploding problem)
而梯度爆炸正好与上图所示的梯度消失的问题正好相反,当 $\text{abs}(w) \ge 1$ 时,那么层数增多的时候,最终的求出的梯度更新将以指数形式增加,即发生梯度爆炸
解决方案
(1)预训练加微调
此方法来自Hinton在2006年发表的一篇论文,Hinton为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程是逐层“预训练”(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。Hinton在训练深度信念网络(Deep Belief Networks中,使用了这个方法,在各层预训练完成后,再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。
(2)梯度横截
梯度横截这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度截断的阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
另外一种解决梯度爆炸的手段是采用权重正则化(weithts regularization)。
(3)使用 Relu 激活函数家族
Relu:思想也很简单,如果激活函数的导数为1,那么就会极大的降低梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
(4)批量标准化(Batch Normalization)
Batchnorm是深度学习发展以来提出的最重要的成果之一了,目前已经被广泛的应用到了各大网络中,具有加速网络收敛速度,提升训练稳定性的效果,Batchnorm本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization,简称BN,即批规范化,通过规范化操作将输出信号x规范化到均值为0,方差为1保证网络的稳定性。
(5)使用残差网络结构
(6)权重初始化时使用高斯初始化
研究方向
BP网络 主要用于以下四个方面。
1)函数逼近:用输入向量和相应的输出向量训练一个网络逼近一个函数。
2)模式识别:用一个待定的输出向量将它与输入向量联系起来。
3)分类:把输入向量所定义的合适方式进行分类。
4)数据压缩:减少输出向量维数以便于传输或存储。
除此之外,在神经网络的可解释性研究方面,向低功耗硬件迁移,以及在认知计算,规划推理等方面和其他传统技术进行结合探索
![[读书笔记]《西瓜书》第五章 神经网络 补充三](https://cdn.jsdelivr.net/gh/Ryuchen/ryuchen.github.io@master/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_700x350_resize_q75_box.jpg)