[读书笔记]《西瓜书》第五章 神经网络 补充三

第五章 神经网络 补充三

神经网络是现在主流的机器学习处理问题的手段，因此需要更加细致的去学习，所以这里自己搜集了一些补充知识点，而且感觉应该需要拆分成几个小章节进行论述，因此这里会使用副标题

激活函数

下面是正式内容开始前的一些总结性的话，感觉容量并不能够单独作为一篇博文，于是就先穿插在这里~

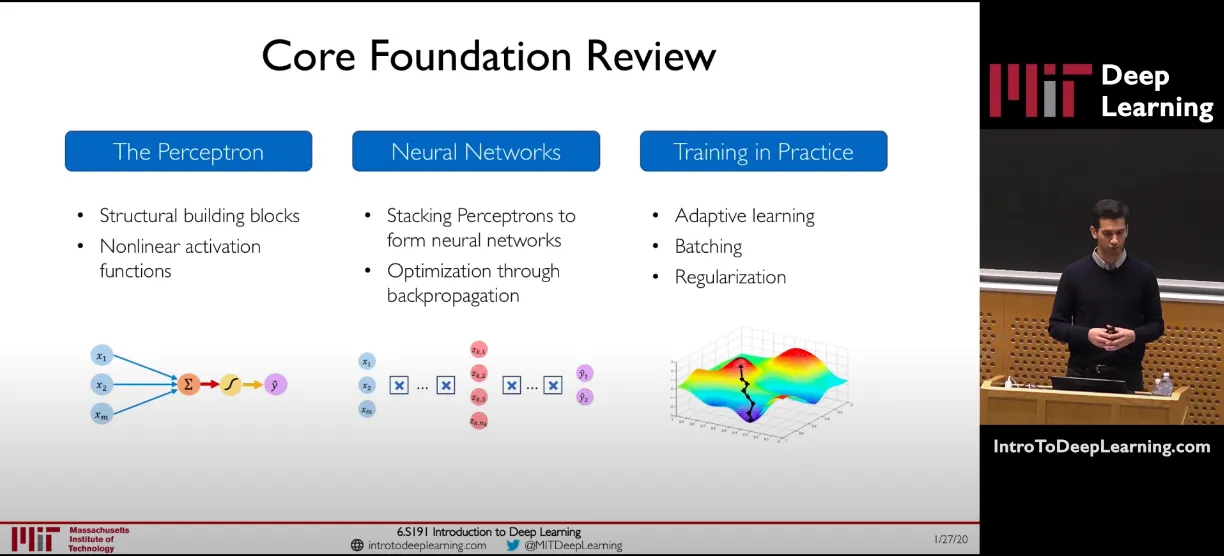
经过前面四篇关于神经网络的博文（呼~关于神经网络模型都写了这么多了，太难了~）了解到了一个简单的神经网络模型构建的基本结构组成可以归纳如下（这里也源自MIT 2020 Deep Learning Camp 的课程）：

• 感知机单元（Perceptron Unit）
  • Structural building blocks
  • Nonlinear activation functions
• 神经网络结构（Neural Networks Architecture）
  • Stacking Perceptrons to form networks
  • Optimization through backpropagation

PS：

• 写这几篇博文的时候，还没有找到过这个视频，所以回顾看下来，感觉自己对于知识点的掌握程度还算是有一定程度的了。😊
• 视频的链接放在了下方Reference里面

o(￣▽￣)ブ~~~~

结合 MIT 这个夏利营的视频，发现基本组织结构跟自己规划博文的内容基本一致，在自己对周志华老师书本内容补充的博文中：《神经网络 铺垫》中介绍了梯度下降的概念，《神经网络 补充一》中介绍了感知机模型，《神经网络 补充二》中介绍了多层感知机与神经网络结构，而后续的篇章的思路基本与这个视频一致，目前的计划将还会分成四篇博文进行阐述激活函数（即本篇博文）、反向传播算法、过拟合问题和why Deep？。至于具体的模型算法，打算是在西瓜书读书笔记写到第九章的时候开始穿插着更新。

OK，接下来书归正传，开始这篇博文的正式内容。

根据上一篇博文的中的描述，我们可以知道激活函数通常是使用非线性函数来进行处理，这也是神经网络中一项很重要的概念，但是我在看到这里的时候同样产生了疑问：

• 为什么需要激活函数？
  • 如果激活函数是线性的会产生什么问题？
• 激活函数有什么基本要求？
• 常见的激活函数有哪些？

为什么需要激活函数？

PS：墙裂推荐知乎这篇问答 神经网络激励函数的作用是什么？有没有形象的解释？

知乎的回答给了非常详细的图示，接下来参考《深入浅出深度学习–原理剖析与Python实践》书中的内容，把数学证明过程记录在此，具体内容可以参见这本书中的内容，给出的证明过程非常清晰。

首先是对于这个问题的具体回答是：如果激活函数是线性的话，那么即使是多层感知机模型(MLP)也仅仅只能够处理线性可分问题，其效果与单层感知机没有任何区别。即神经网络模型之所以学习能力得到了提高，本质上并不是因为层次加深带来的效果，而是因为在层次中引入了非线性的激活函数。

数学证明

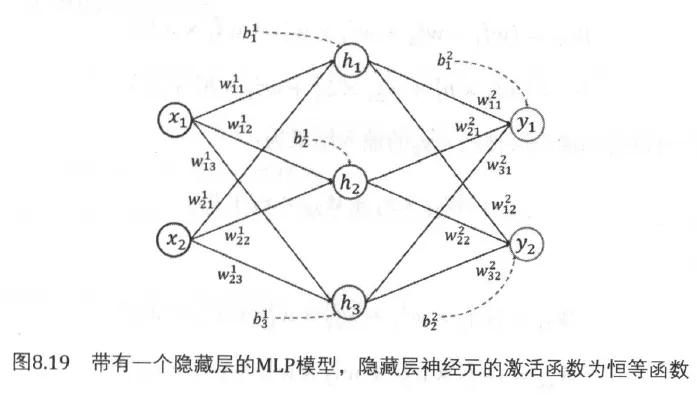
这是一个有一个隐藏层，并且在隐藏层中包含三个神经元的简单多层感知机（MLP）模型或者也可以曾称呼为前馈人工神经网络（FFANN）模型，为了接下来证明的方便，采用最简单的线性函数 $f(x) = x$ 来作为激活函数。

隐藏层的输入为：

$$ h_1 = w_{11}^1 * x_1 + w_{21}^1 * x_2 + b_1^1 \\
h_2 = w_{12}^1 * x_1 + w_{22}^1 * x_2 + b_2^1 \\
h_3 = w_{13}^1 * x_1 + w_{23}^1 * x_2 + b_3^1 $$

由于激活函数是恒等函数，因此，经过激活函数的处理后，输入与输出是一致的，即： $$ a_1 = h1, a_2 = h_2, a_3 = h_3 $$ 于是我们可以得到 $y_1$ 的输出为： $$ \begin{align} y_1 & = & w_{11}^2 * a_1 + w_{21}^2 * a_2 + w_{31}^2 * a_3 + b_1^2 \\
& = & w_{11}^2 * (w_{11}^1 * x_1 + w_{21}^1 * x_2 + b_1^1) \\
& & + w_{21}^2 * (w_{12}^1 * x_1 + w_{22}^1 * x_2 + b_2^1) \\
& & + w_{31}^2 * (w_{13}^1 * x_1 + w_{23}^1 * x_2 + b_3^1) \\
& = & \boldsymbol{w}_{11} * x_1 + \boldsymbol{w}_{12} * x_2 + \boldsymbol{b}_1 \end{align} $$

则展开化简后可以得到： $$ \boldsymbol{w}{11} = (w{11}^2 * w_{11}^1 + w_{21}^2 * w_{12}^1 + w_{31}^2 * w_{13}^1) \\
\boldsymbol{w}_{12} = (w_{11}^2 * w_{21}^1 + w_{21}^2 * w_{22}^1 + w_{31}^2 * w_{23}^1) \\
\boldsymbol{b}_1 = (w_{11}^2 * b_1^1 + w_{21}^2 * b_2^1 + w_{31}^2 * b_3^1 + b_1^2) $$

同样，同理也可以求出 $y_2$ 的神经元的输出，这里就略过不写了，但是基本上可以看的出来来，其实只是系数进行了非线性的关联叠加，但是有因为系数是常数，所以直接求其之后和值和逐层求解本质上没有增加任何的学习能力。

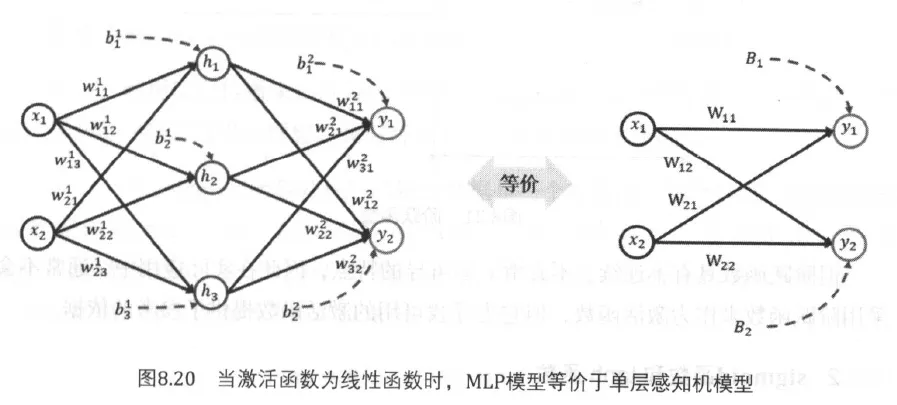
激活函数有什么基本要求？

既然结合上一篇文章的内容和前面所说的内容，那么我们该如何选择激活函数呢？

首先是激活函数的来源是仿照生物神经元的思想，试图将输入与输出之间通过激活函数的处理后，呈现两个状态，即神经元的激活状态和抑制状态，因此其最根本的要求是能够将任意的输入值映射到二值之间~ 因此 跃阶函数 $\text{sign}(·)$ 就是一个理想的解决方案，但是前面也提到了，我们在对模型求解最优解的时候，需要使用梯度下降法，来进行模型损失函数的偏导求解，于是这里就有了使用 $\text{sigmoid}(·)$ 函数的想法，具体在前文线性模型中就已经介绍过了。

纵观现在的激活函数来看，其基本性质可以概括以下两点：

• 函数形态应该在两端是饱和（变成常量）而在中间点快速切换
• 能够求导以方便计算梯度

常见的激活函数有哪些？

在这里的时候，本来是打算在网络上尽可能搜集全的，发现大多数的博文中都是只简单介绍了几种，不过幸运的是，竟然找到了一个博客，将近二十种的激活函数进行了整理，所以这里我也就不进行整理了，将其博文的地址引用在这里。

Visualising Activation Functions in Neural Networks

PS: 为了方便理解和后续自己的查看，这里将博主在图中的注释进行一下解释

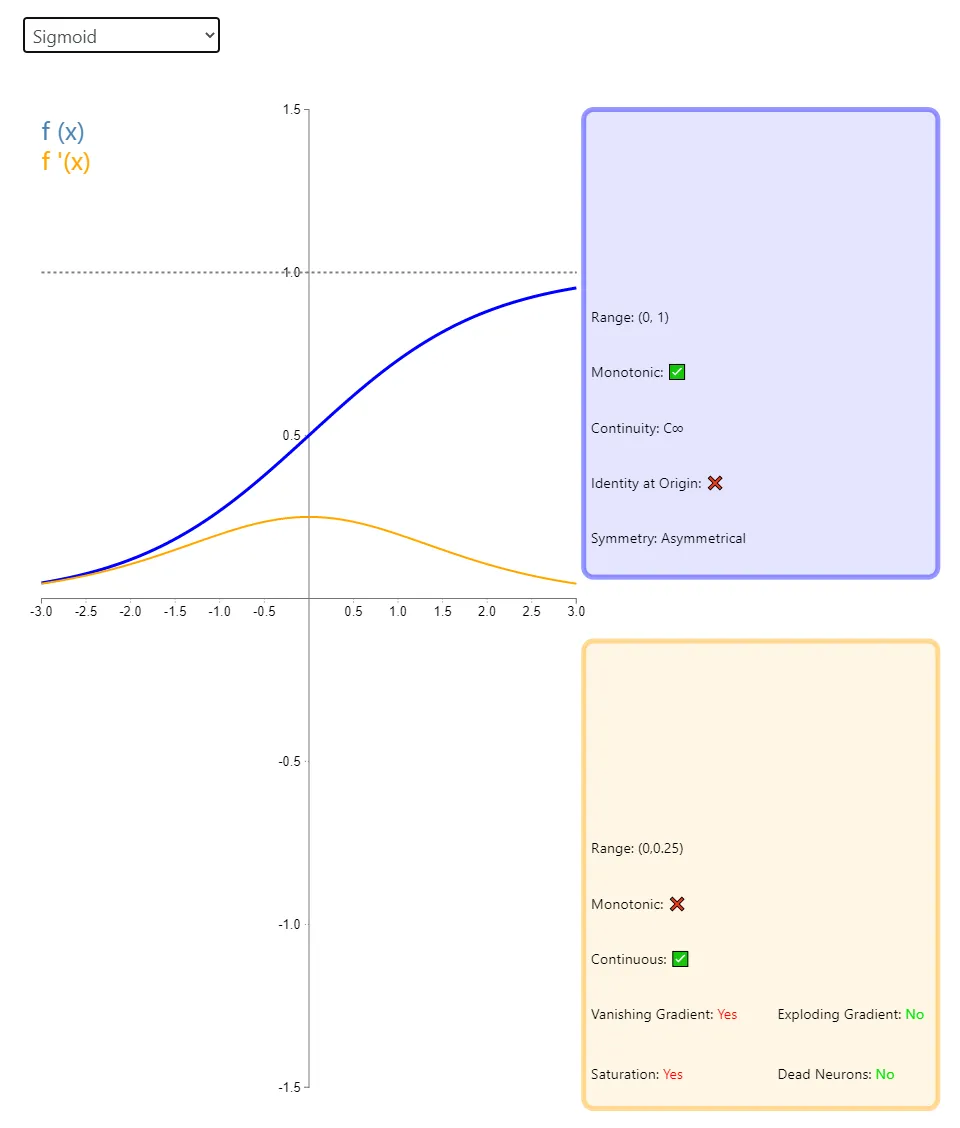
图示为选择 Sigmoid 为激活函数时其展示的图像

• 蓝色的表示Sigmoid的函数图像
  • Range 表示值域
  • Monotonic 表示是否单调
  • Continuity 表示是否连续
  • Identity at Origin 通过原点进行区分
  • Symmetry 图像是否对称
• 黄色的表示对其求导后的函数图像
  • Range 表示值域
  • Monotonic 表示是否单调
  • Continuity 表示是否连续
  • Vanishing Gradient 是否存在梯度消失问题
  • Exploding Gradient 是否存在梯度爆炸问题
  • Saturation 是否在两端会出现饱和问题
  • Dead Neurons 是否会面临神经元失活的问题

Reference

• MIT Deep Learning
• 神经网络激励函数的作用是什么？有没有形象的解释？
• Visualising Activation Functions in Neural Networks
• 《深入浅出深度学习–原理剖析与Python实践》
• Understanding Activation Functions in Neural Networks
• 26种神经网络激活函数可视化（上面 Visualising Activation Function 的中文版截图）