[读书笔记]《西瓜书》第五章 神经网络 补充二
![[读书笔记]《西瓜书》第五章 神经网络 补充二](/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_900x500_fit_q75_box.jpg)
第五章 神经网络 补充二
神经网络是现在主流的机器学习处理问题的手段,因此需要更加细致的去学习,所以这里自己搜集了一些补充知识点,而且感觉应该需要拆分成几个小章节进行论述,因此这里会使用副标题
神经网络模型
周老师的西瓜书中没有明确点出多层感知机和神经网络的具体概念,只是说感知机模型叠加多层以后能够解决样本集合一些非线性的问题,然后涉猎了一下神经网络模型的几个概念就简单结束了。所以在这里我也是问题驱动式的去想到了一些问题,然后为了解决这些问题去进行了资料搜集,补充在这篇博文中。
- 多层感知机的具体定义是什么?
- 多层感知机和神经网络的有什么关联?
多层感知机(Multilayer Perceptron)
这里对于多层感知机的定义,本人找了几个,首先在《Dive into Deep Learning》这本书中给出的定义基本和西瓜书上是一致的,只不过是把西瓜书中明确给出的定义表述了一遍。
多层感知机在单层神经网络的基础上引入了一到多个隐藏层(hidden layer)。隐藏层位于输入层和输出层之间。
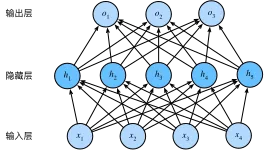
此外还找了一下wikipedia上关于多层感知机的定义描述。
A multilayer perceptron (MLP) is a class of feedforward artificial neural network (ANN). The term MLP is used ambiguously, sometimes loosely to any feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons (with threshold activation). Multilayer perceptrons are sometimes colloquially referred to as “vanilla” neural networks, especially when they have a single hidden layer.[1]
An MLP consists of at least three layers of nodes: an input layer, a hidden layer and an output layer. Except for the input nodes, each node is a neuron that uses a nonlinear activation function. MLP utilizes a supervised learning technique called backpropagation for training.[2][3] Its multiple layers and non-linear activation distinguish MLP from a linear perceptron. It can distinguish data that is not linearly separable.[4]
感知机模型是前馈人工神经网络(FFANN)中的一种。术语MLP的使用非常的混杂,有时可以宽泛的指代任何前馈神经网络模型,有时却特指由多层的感知机模型(有阈值和激活函数)组成的多层网络结构。多层感知机有时会被通俗的称之为‘香草’神经网络(即,原始神经网络),特别是在它只有一个隐层的时候。
多层感知机模型至少由三层结构组成:输入层、隐层和输出层。其中除了输入层的节点外,其他层中的神经元节点都拥有一个非线性的激活函数。多层感知机模型使用监督学习中的技术–反向传播算法,用来作为模型的训练手段。区别于线性感知机算法,多层感知机模型能够在非线性激活函数的基础下处理非线性可分的数据集。
看到这里想到李宏毅老师层说过:多层感知器可以实现非线性判别,如果用于回归,可以逼近输入的非线性函数,已经证明,具有一个隐藏层(隐藏节点个数不限)的MLP可以学习输入的任意非线性函数。
OK,有了上面两个定义了,这里就可以得出一些简单的结论了,至于结论是否正确,有些存疑的地方我并没有查到相关的资料来证否,所以暂定结论如下:
- 多层感知机算法是监督学习的算法模型
- 多层感知机的结构为三层或者以上的神经元结构组成,即西瓜书中说到的,至少包含一个隐层结构
- 多层感知机模型可以处理分线性可分问题
- 多层感知机模型中使用的激活函数为非线性激活函数
多层感知机的本质
既然多层感知机能够解决非线性问题,那么它是如何解决异或问题的呢?
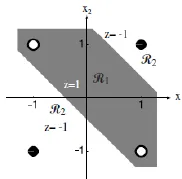
西瓜书和网上随处可以搜到这个示意图,但是多层感知机就是找到两条线将其进行类别划分吗?我也在网上找了很多资料,然后发现了Eason.wxd大佬在其博文中给出了直观的图示答案。
单个感知器虽然无法解决异或问题,但却可以通过将多个感知器组合,实现复杂空间的分割。如下图:
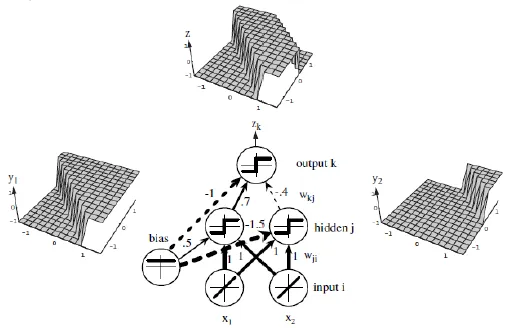
将两层感知器按照一定的结构和系数进行组合,第一层感知器实现两个线性分类器,把特征空间分割,而在这两个感知器的输出之上再加一层感知器,就可以实现异或运算。也就是,由多个感知器组合:
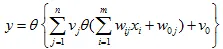
来实现非线性分类面,其中 $\theta$ 表示阶跃函数或符号函数。
心满意足,了解了多层感知机的定义和实质,之后就继续解决下一个问题,多层感知机和神经网络的有什么关联?
神经网络(Neural Networks)
其实根据上面找到的资料,已经可以得到一个结论了,即多层感知机模型其实是神经网络家族下面的一个种类中的特例,即在前馈神经网络模型中的一种。
前馈神经网络的定义
A feedforward neural network is an artificial neural network wherein connections between the nodes do not form a cycle.[1] As such, it is different from its descendant: recurrent neural networks.
The feedforward neural network was the first and simplest type of artificial neural network devised.[2] In this network, the information moves in only one direction—forward—from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.[1]
前馈神经网络是人工神经网络中一类没有神经元节点之间相互连接形成环路的结构。相对应的,与递归神经网络就是不相同的。
前馈神经网络是设计的第一种也是最简单的一种人工神经网络。在这个网络模型中,信息只在一个方向上前向移动,即从输入节点到隐藏节点再到输出节点,网络中不存在周期与循环的结构。
研究内容
当然大的方面上,神经网络的研究内容要宽泛的多,也不是个人能学会的东西。立足于西瓜书在后续给出的几个特别常见的神经网络模型看来,对于神经网络模型的研究有一个方向,即如何确定神经网络的结构,比如常见的:CNN,RNN,ResNet 和 LSTM等等,都是对神经网络模型的结构进行了创新。
当然网络结构的创新,日新月异了,但是主要有两点还是比较令人关注的点,即如何确定神经网络的隐层数与每个隐层的节点个数。
这里网上有很多讨论的文章,这里就摘抄一下 Eason.wxd 的博客内容
隐层数
一般认为,增加隐层数可以降低网络误差(也有文献认为不一定能有效降低),提高精度,但也使网络复杂化,从而增加了网络的训练时间和出现“过拟合”的倾向。**Hornik 等早已证明:若输入层和输出层采用线性转换函数,隐层采用Sigmoid转换函数,则含一个隐层的MLP网络能够以任意精度逼近任何有理函数。**显然,这是一个存在性结论。在设计BP网络时可参考这一点,应优先考虑3层BP网络(即有1个隐层)。一般地,靠增加隐层节点数来获得较低的误差,其训练效果要比增加隐层数更容易实现。对于没有隐层的神经网络模型,实际上就是一个线性或非线性(取决于输出层采用线性或非线性转换函数型式)回归模型。因此,一般认为,应将不含隐层的网络模型归入回归分析中,技术已很成熟,没有必要在神经网络理论中再讨论之。
隐层节点数
在 BP 网络中,隐层节点数的选择非常重要,它不仅对建立的神经网络模型的性能影响很大,而且是训练时出现“过拟合”的直接原因,但是目前理论上还没有一种科学的和普遍的确定方法。
目前多数文献中提出的确定隐层节点数的计算公式都是针对训练样本任意多的情况,而且多数是针对最不利的情况,一般工程实践中很难满足,不宜采用。事实上,各种计算公式得到的隐层节点数有时相差几倍甚至上百倍。为尽可能避免训练时出现“过拟合”现象,保证足够高的网络性能和泛化能力,确定隐层节点数的最基本原则是:在满足精度要求的前提下取尽可能紧凑的结构,即取尽可能少的隐层节点数。研究表明,隐层节点数不仅与输入/输出层的节点数有关,更与需解决的问题的复杂程度和转换函数的型式以及样本数据的特性等因素有关。
在确定隐层节点数时必须满足下列条件:
(1)隐层节点数必须小于N-1(其中N为训练样本数),否则,网络模型的系统误差与训练样本的特性无关而趋于零,即建立的网络模型没有泛化能力,也没有任何实用价值。同理可推得:输入层的节点数(变量数)必须小于N-1。
(2)训练样本数必须多于网络模型的连接权数,一般为2~10倍,否则,样本必须分成几部分并采用“轮流训练”的方法才可能得到可靠的神经网络模型。
总之,若隐层节点数太少,网络可能根本不能训练或网络性能很差;若隐层节点数太多,虽然可使网络的系统误差减小,但一方面使网络训练时间延长,另一方面,训练容易陷入局部极小点而得不到最优点,也是训练时出现“过拟合”的内在原因。因此,合理隐层节点数应在综合考虑网络结构复杂程度和误差大小的情况下用节点删除法和扩张法确定。
![[读书笔记]《西瓜书》第五章 神经网络 补充一](https://cdn.jsdelivr.net/gh/Ryuchen/ryuchen.github.io@master/images/machine-learning_huda146d3825fc6d502e05b38609bff098_23368_700x350_resize_q75_box.jpg)