[读书笔记]《西瓜书》第五章 神经网络 补充一

第五章 神经网络 补充一

神经网络是现在主流的机器学习处理问题的手段，因此需要更加细致的去学习，所以这里自己搜集了一些补充知识点，而且感觉应该需要拆分成几个小章节进行论述，因此这里会使用副标题

感知机模型

线性可分和异或问题

“Although the perceptron rule finds a successful weight vector when the training examples are linearly separable, it can fail to converge if the examples are not linearly separable.” – quote from 《Machine Learning book》 by Tom Mitchell

在学习西瓜书的时候，书中提到了一个知识概念并进行了补充：线性可分问题。在书中给出的答案是：若两类模式是线性可分的，即存在一个线性超平面能将它们分开？然后给出了一个特别代表性的例子：异或问题。

然后对这里个人是产生了比较浓厚的兴趣，究竟什么是线性可分（linearly separable）？

线性可分

在找到的众多答案中，个人感觉还是wikipedia的解答最好，于是摘录在下面

In Euclidean geometry, linear separability is a property of two sets of points. This is most easily visualized in two dimensions (the Euclidean plane) by thinking of one set of points as being colored blue and the other set of points as being colored red. These two sets are linearly separable if there exists at least one line in the plane with all of the blue points on one side of the line and all the red points on the other side. This idea immediately generalizes to higher-dimensional Euclidean spaces if the line is replaced by a hyperplane.

The problem of determining if a pair of sets is linearly separable and finding a separating hyperplane if they are, arises in several areas. In statistics and machine learning, classifying certain types of data is a problem for which good algorithms exist that are based on this concept. – quote from WIKIPEDIA

其实很好理解的一个问题，相信每一个学习机器学习的人都知道这个概念。然后各种书籍中都常见的如下的这种示意图

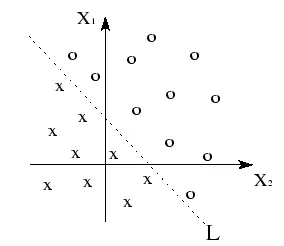
假设我们想要将拥有两个特征的数据集 $(X_1，X_2)$ 分为两类，如图上图所示。 每个带有 $x$ 或 $o$ 符号的点代表一个带有一组 $(X_1，X_2)$ 值的样例。 在这里每个样例都可以被分为两类其中一个，并注意，同时这两个类别可以用一条直线 $L$ 分隔开来。则它们被称为线性可分。

线性可分性是指：具有 $n$ 维特征 $\boldsymbol{x}=(x_1，x_2，…，x_n)$ 的样例的类别可以通过单个决策面 $L$ 进行分离。

但是这里本人是产生了两个疑问？

• 线性可分的前提条件一定是欧几里得空间吗？
• 为什么要强调线性可分性的问题？

问题的来源

首先第一个问题是源自个人在学习机器学习的同时也在恶补线性代数的知识（PS：单独学线性代数真的好难，但是借助机器学习的过程去学别有一番风味，更好的理解），所以时常会在学习的过程中去问这个模型的假设空间是什么？即个人感觉特别需要注意的是：如果是欧几里得空间的话，则其在样本的特征选择上面就必须是相互独立的特征，否则在具体实际操作模型训练的时候可能会出现问题~

其次第二个问题是源自B站shuhuai008大佬的视频，在其讲解感知机算法的视频中，强调了明斯基在当年就提出感知机模型无法解决非线性可分问题，那么为啥当年明斯基要这么强调线性可分问题呢？

问题的解决

当然自己也尝试去找了这两个问题的答案，

首先是第一个问题，作者这里没有在网上找到答案，能够搜集到问题描述都是建立在欧几里得空间的或者是完全不提欧式空间这个前提，所以如果您有相关的见解的话，可以给我的博客下面留言，感谢~

然后是第二个问题，当然在这个问题上找到了我理想中的答案，也是一位台大老师–林轩田的视频《机器学习基石》个人觉得非常值得看一看，虽然是一个很容易忽略的问题，但是这个问题非常的重要，竟然关联除了机器学习为什么会生效的哲学问题~

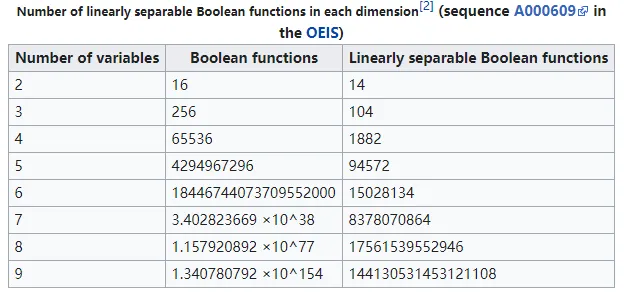
这里引用一下wikipedia上的示例：

A Boolean function in n variables can be thought of as an assignment of 0 or 1 to each vertex of a Boolean hypercube in n dimensions. This gives a natural division of the vertices into two sets. The Boolean function is said to be linearly separable provided these two sets of points are linearly separable. The number of distinct Boolean functions is ${\displaystyle 2^{2^{n}}}$ where n is the number of variables passed into the function.[1]

异或问题

正如西瓜书中举的例子一样，逻辑运算中的异或问题常常被用来当作最简单的非线性问题举例子

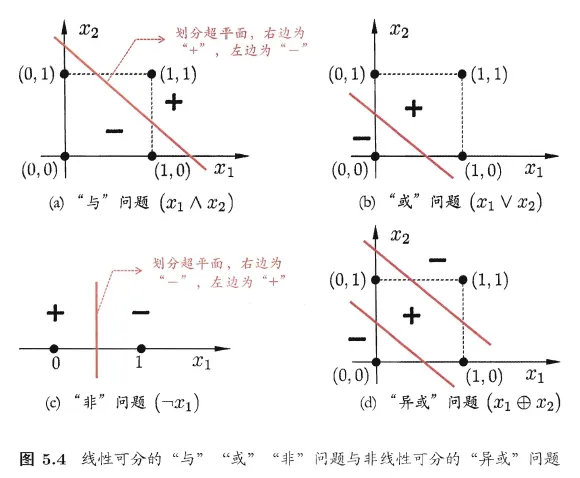
即在异或（Exclusive-OR）状况下的样本点，无法使用一条直线将其分开，但其实异或可以用与、或、非三个线性问题进行表示：

$${\displaystyle {\begin{matrix}p\oplus q&=&(p\land \lnot q)&\lor &(\lnot p\land q)\\[3pt]&=&((p\land \lnot q)\lor \lnot p)&\land &((p\land \lnot q)\lor q)\\[3pt]&=&((p\lor \lnot p)\land (\lnot q\lor \lnot p))&\land &((p\lor q)\land (\lnot q\lor q))\\[3pt]&=&(\lnot p\lor \lnot q)&\land &(p\lor q)\\[3pt]&=&\lnot (p\land q)&\land &(p\lor q)\end{matrix}}}$$

书中提到当简单的两层感知机就能解决异或问题，那么是如何解决的呢？

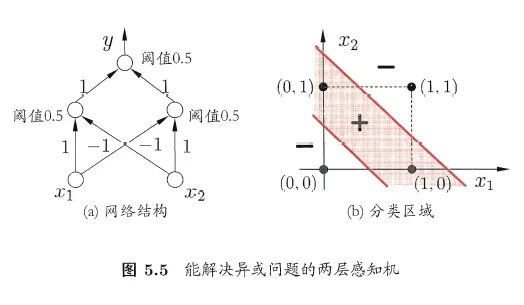
书中给了上示的图例，可以看出当使用两层感知机模型的时候，这个时候问题的解决空间是以两个直线进行划分的了~ 看到这里的时候有没有突然引发你一个问题？

那么三层感知机的时候对样本的划分是什么样的呢？

在这里这个问题后续博文中再说~

感知机模型

小历史：

1957年，感知机算法Perceptron的发明，使用MCP模型对多维输入做二分类，梯度下降法学习权重。感知机算法的思想很简单，即通过样本正确与否调整分类面，使得分类面对样本的分类误差最小。该算法是神经网络和支持向量机的基础，随后被证明能够收敛，其理论和实践效果引发了第一次神经网络浪潮。

1969年，美国数学家和人工智能先驱Minsky证明了感知机是一种线性模型，它只能处理线性分类问题，比如简单的异或问题（XOR）就解决不了。

PS: 虽然机器学习书里面提到了感知机模型，但是其描述的不够详细，以下的内容整理自李航老师的《统计机器学习》

模型的定义

感知机(perceptron)是二类分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取+1和-1二值。感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面，属于判别模型。

模型的目的

感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。

模型的特点

感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式。

感知机1957年由 Rosenblat提出,是神经网络与支持向量机的基础。

虽然书中这么写，看着会让人有点绕晕，但是其实本质上很简单，整合在一起就是小学的数学公式，即

$${f(\boldsymbol{x})={\begin{cases}1&{\text{if}}\ \boldsymbol{w} \cdot \boldsymbol{x} + b > 0,\ 0&{\text{otherwise}}\end{cases}}}$$

用图形化的界面来演示的话，即

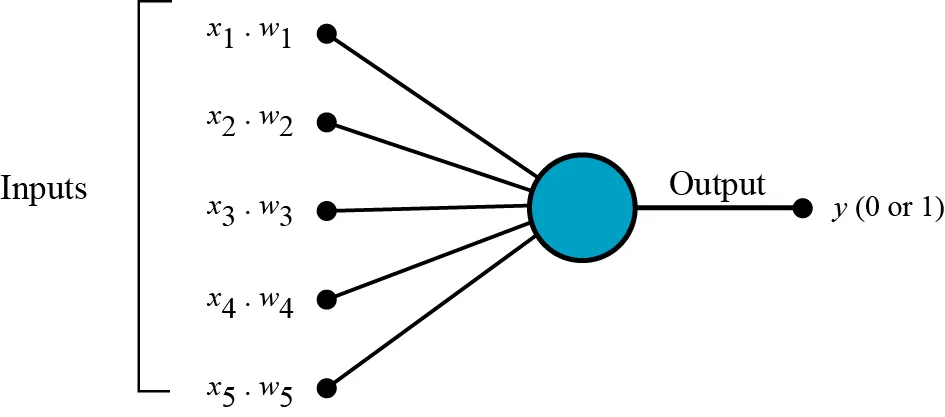
整个模型的直观展示的话，就是如下图，即

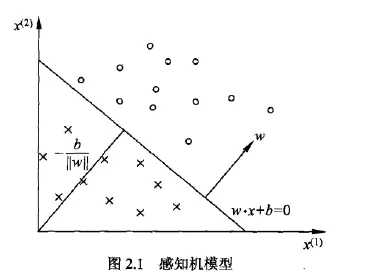
李航老师书中给了两个感知机算法的形式，记录如下

原始形式

对偶形式

感知机家族

• Pocket PLA：在搜寻最佳分类直线的时候，随机选择错误点修正，修正后的直线放在口袋里，暂时作为最佳分类线。然后如果还有错误点，继续随机选择某个错误点修正，修正后的直线与口袋里的分类线比较，把分类错误点较少的分类线放入口袋。一直到迭代次数结束，这时候放在口袋里的一定是最佳分类线，虽然可能还有错误点存在，但已经是最少的了。
• Voted Perceptron
• Perceptron with margin
• Average PLA：其学习的过程，与Perceptron感知器的基本相同，只不过，它将所有的训练过程中的权值都保留下来，然后，求均值。它的优点是克服由于学习速率过大，所引起的训练过程中出现的震荡现象。即超平面围着一个中心，忽左忽右之类。

Reference

• Linear separability
• Perceptron
• Linear Separability and the XOR Problem
• 如何理解「异或」的含义？
• Percetron
• What the Hell is Perceptron?