[读书笔记]《西瓜书》第五章 神经网络 铺垫

梯度下降

---

在第三章节中，学习了线性模型中的线性回归，当时使用的最小二乘法来进行模型的拟合求解，那么对于神经网络里面的模型来说，是否也有最小二乘法一样的方式来进行模型拟合呢？对于这个问题的解答，就是需要在神经网络章节开始之前进行的知识铺垫了，即梯度下降算法（Gradient Descent）

PS: 这里梯度下降算法，强烈推荐台大李宏毅老师的视频讲解，不仅浅显易懂而且还把相关求解算法模型串联了一遍，真的是强无敌~

梯度下降（Gradient Descent）

首先第一个问题显而易见的就是什么是梯度下降算法？这个问题我也是收集了很多的书籍和资料，但是没能找到一个令我很满意的解答，不过有一个论坛的回答我个人觉得还是相对比较好的，于是引用在下

---

Basically the ‘gradient descent’ algorithm is a general optimization technique and can be used to optimize ANY cost function. It is often used when the optimum point cannot be estimated in a closed form solution.

So let’s say we want to minimize a cost function. What ends up happening in gradient descent is that we start from some random initial point and we try to move in the ‘gradient direction’ in order to decrease the cost function. We move step by step until there is no decrease in the cost function. At this time we are at the minimum point. To make it easier to understand, imagine a bowl and a ball. If we drop the ball from some initial point on the bowl it will move until it is settled at the bottom of the bowl.

— quote by stackoverflow answer

---

这里我大概以自己的理解翻译一下：

基本上“梯度下降”算法是一种通用的优化技术，可用于优化任何成本函数。当无法构建一个闭式解来从中估计最佳点时，通常使用它。

假设我们要最小化代价函数。梯度下降操作的结果是，我们从某个随机的初始点开始，然后尝试沿“梯度方向”移动，以降低代价函数。我们一步一步地前进，直到代价函数不再降低。目前，我们处于最低点。为了更容易理解，请想象一个碗和一个球。如果我们将球从碗上的某个起始点放下，它将移动，直到它落在碗的底部。

当然网上也有各种讲解的视频，比较好的就是3blue1brown，视频我也引用在下面：

不过这里就引出了两个问题，一个是什么是闭式解？一个是在前面章节中用来求解均方误差的最小二乘法，它和梯度下降法有什么区别？

闭式解与数值解

这里定义也是网络上随处可以找得到的，于是找了一个定义放在了下面。

解析解(analytical solution)：

​ 就是一些严格的公式，给出任意的自变量就可以求出其因变量，也就是问题的解。他人可以利用这些公式计算各自的问题。所谓的解析解是一种包含：分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式。用来求得解析解的方法称为解析法〈analytic techniques、analytic methods〉，解析法即是常见的微积分技巧，例如分离变量法等。解析解为一封闭形式〈closed-form〉的函数，因此对任一独立变量，我们皆可将其带入解析函数求得正确的相依变量。因此，解析解也被称为闭式解（closed-form solution）。

数值解(numerical solution)：

​ 是采用某种计算方法，如有限元的方法，数值逼近，插值的方法，得到的解。别人只能利用数值计算的结果，而不能随意给出自变量并求出计算值。当无法藉由微积分技巧求得解析解时，这时便只能利用数值分析的方式来求得其数值解了。数值方法变成了求解过程重要的媒介。在数值分析的过程中，首先会将原方程式加以简化，以利后来的数值分析。例如，会先将微分符号（连续）改为差分符号（离散）等。然后再用传统的代数方法将原方程式改写成另一方便求解的形式。这时的求解步骤就是将一独立变量带入，求得相依变量的近似解。因此利用此方法所求得的相依变量为一个个分离的数值〈discrete values〉，不似解析解为一连续的分布，而且因为经过上述简化的动作，所以可以想见正确性将不如解析法来的好。

解析解就是对于一个问题的求解，所得到的结果的解是一个函数表达式，而不是一个具体的数值或者数据，只要在这个结果函数表达式中再代入具体数值，就可以求得对应问题的数值解。

数值解则是对于问题的求解结果是一个实实在在的具体的数值或者数据，使用者不能再对这个数值或者数据做任何数值计算或化简等操作，只能利用这个数值或者数据进行分析评估计算的准确性或者是否正确表达了某个问题。

最小二乘法 VS 梯度下降法

回顾第三章线性模型中的最小二乘法给出的定义和公式，可以看到最小二乘法是相当的简洁和高效的，但是为什么现在在机器学习领域我们通常在线性回归中使用梯度下降法来取代最小二乘法呢？难道我们直接求 $\boldsymbol{w}=(X^TX)^{-1}X^T\boldsymbol{y}$ 得到结果不香吗？

这里就要把之前线性模型补充的内容引用过来一下了。

---

There are four principal assumptions which justify the use of linear regression models for purposes of inference or prediction:

• linearity and additivity of the relationship between dependent and independent variables:
  • (a) The expected value of dependent variable is a straight-line function of each independent variable, holding the others fixed.
  • (b) The slope of that line does not depend on the values of the other variables.
  • (c) The effects of different independent variables on the expected value of the dependent variable are additive.
• statistical independence of the errors (in particular, no correlation between consecutive errors in the case of time series data)
• homoscedasticity (constant variance) of the errors
  • (a) versus time (in the case of time series data)
  • (b) versus the predictions
  • (c) versus any independent variable
• normality of the error distribution.

---

第一，最小二乘法需要计算的逆矩阵，有可能它的逆矩阵不存在，这样就没有办法直接用最小二乘法了，此时梯度下降法仍然可以使用。当然，我们可以通过对样本数据进行整理，去掉冗余特征。让的行列式不为0，然后继续使用最小二乘法。

第二，当样本特征n非常的大的时候，计算的逆矩阵是一个非常耗时的工作（nxn的矩阵求逆），甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。那这个n到底多大就不适合最小二乘法呢？如果你没有很多的分布式大数据计算资源，建议超过10000个特征就用迭代法吧。或者通过主成分分析降低特征的维度后再用最小二乘法。

第三，如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用，此时梯度下降仍然可以用。

第四，讲一些特殊情况。当样本量m很少，小于特征数n的时候，这时拟合方程是欠定的，常用的优化方法都无法去拟合数据。当样本量m等于特征说n的时候，用方程组求解就可以了。当m大于n时，拟合方程是超定的，也就是我们常用与最小二乘法的场景了。

— quota by 最小二乘法小结

这里本来想自己整理写的，但是在搜集资料的时候找到了大佬给出的答案，跟自己的思路一致，于是就引用在这里了~

梯度下降法详解

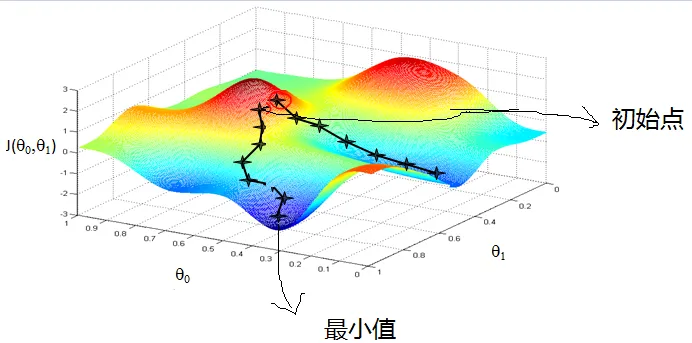
这里虽然是详细解释梯度下降算法，但是也不需要做太细的讲解，我认为吴恩达老师和李宏毅老师的视频讲解足够的清晰明了了，相关的视频链接在下面，这里我只把自己认为重要的简单记录在下方，希望对自己会议和读者有帮助：

相关概念

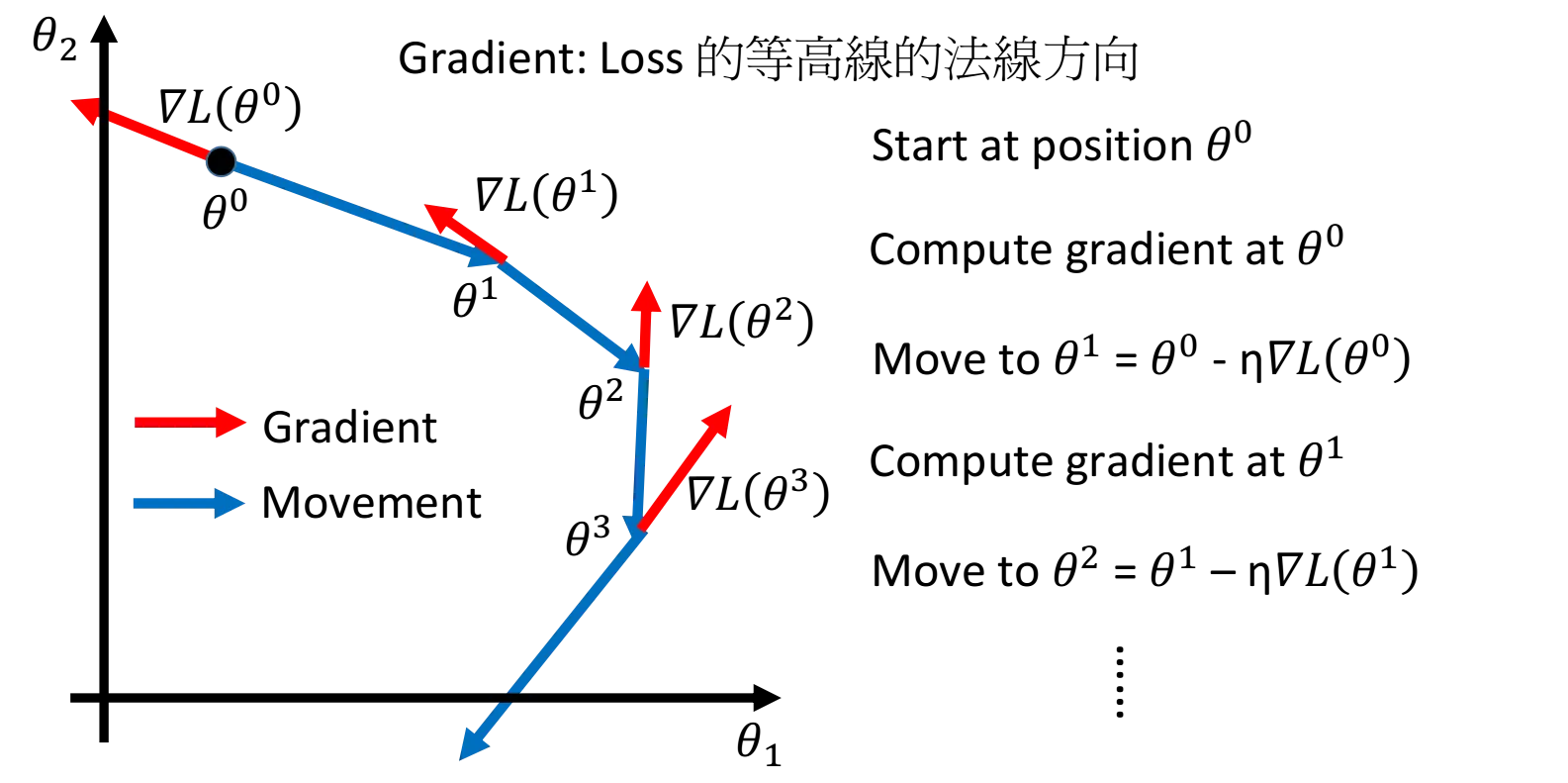
方向：即导数的反方向

大小：即每次移动到下个点的步长

局部最优：即到达的最低点也并不一定是全局下的最低点

PS: 通常情况下，导数的反方向是下降最快的方向，而步长最理想的情况即为当前点到达最低点的间隔

算法调优？

如何解决方向、大小的选择问题和避免局部最优的陷阱即为算法的调优过程，其对应的点即围绕着上面的三个相关概念展开

1. 算法的步长选择。在步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。 初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
3. 算法的迭代次数大小。可以想象的到在一种理想的情况下，如果我们选择了非常理想的步长和初始值，恰好我们能找到全局最优解，但是我们要迭代多少次呢？过早还没到，过多的话造成时间的浪费。
4. 特征的缩放。这一部分也是十分关键，在李宏毅老师的视频中提到过，如果我们的特征尺度不一样，那么我们在选择前面三个参数的时候就需要特别的小心。

简单概括一下就是：Start Point、Learning Rate、Iteration 和 Feature scaling

更详细的解释参考知乎答案，老董老师的解答：梯度下降的参数更新公式是如何确定的？

家族模型

前人们为了解决这个问题可谓是脑洞大开，为我们开辟出了众多算法模型，所以梯度下降算法也是一个大的家族，下面罗列一些这个大家族中的算法模型。

针对更新频度

• 批量梯度下降法（Batch Gradient Descent）：是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。

• 随机梯度下降法（Stochastic Gradient Descent）：随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本来求梯度。

• 小批量梯度下降法（Mini-batch Gradient Descent）：小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷，也就是对于 $m$ 个样本，我们采用 $x$ 个样本来迭代，$1<x<m$ 。

针对更新步长

• NAG（Nesterov accelerated gradient）：NAG首先向先前累积的梯度（棕色矢量）的方向大跳，测量梯度，然后进行校正（红色矢量），这将导致完整的NAG更新（绿色矢量）。

• Adagrad：是一种基于梯度的优化算法，它做到使学习率适应参数，对与频繁出现的特征参数执行较小的更新（即低学习率），并对不常出现的特征参数进行较大的更新（即高学习）。采用的方法是累计过去所有的平方梯度作为学习率的底以此来以次数的角度控制学习率的迭代过程。

• Adadelta：是Adagrad的扩展，旨在降低其激进的，单调降低的学习率。 Adadelta不会累计所有过去的平方梯度，而是将累计过去的梯度的窗口限制为某个固定大小值。

• RMSprop：RMSprop和Adadelta都是在大约同一时间独立开发的，其原因是需要解决Adagrad的学习率急剧下降的问题。 RMSprop将学习率除以平方梯度的指数衰减平均值。

针对局部最优

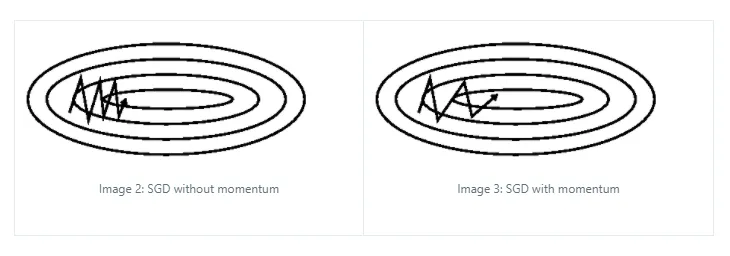
• Momentum：是一种有助于在相关方向上加速SGD并抑制振荡的方法。它通过添加一个分量来实现过去时间步的更新向量到当前更新向量的关系。

相互结合的方式

• Adam：Adam为每个参数计算自适应学习率。 除了存储像Adadelta和RMSprop这样的过去平方梯度vt的指数衰减平均值之外，Adam还保留了过去梯度的指数衰减平均值，类似于Momentum。
• Nadam：Adam可以看作是RMSprop和Momentum的组合。我们还看到，Nesterov accelerated gradient（NAG）优于vanilla momentum。 Nadam（Nesterov-accelerated Adaptive Moment Estimation）因此可以看作是结合了Adam 和 NAG。

更加详细的说明请参见 外国SEBASTIAN RUDER大佬的博文An overview of gradient descent optimization algorithms，以上内容均来自其博文内容中整理的知识点，但是不够全，强烈建议把其博文看一遍~

特征缩放

这里特意的忽略一下，因为这里我觉得有必要展开记录一下，因为在之前的全国数模比赛中，就发现特征缩放对于数据集在什么情况下如何使用都是一门大学问~

理论基础（补充一点）

这里的内容也是源自李宏毅老师视频讲解，个人觉得还是很有必要记忆一下的

泰勒展开式：

$$f(x)=\frac{f(a)}{0!}+\frac{f^{'}(a)}{1!}(x-a)+\frac{f^{''}(a)}{2!}(x-a)^2+\frac{f^{(n)}(a)}{n!}(x-a)^n+\cdots+R_n(x)$$

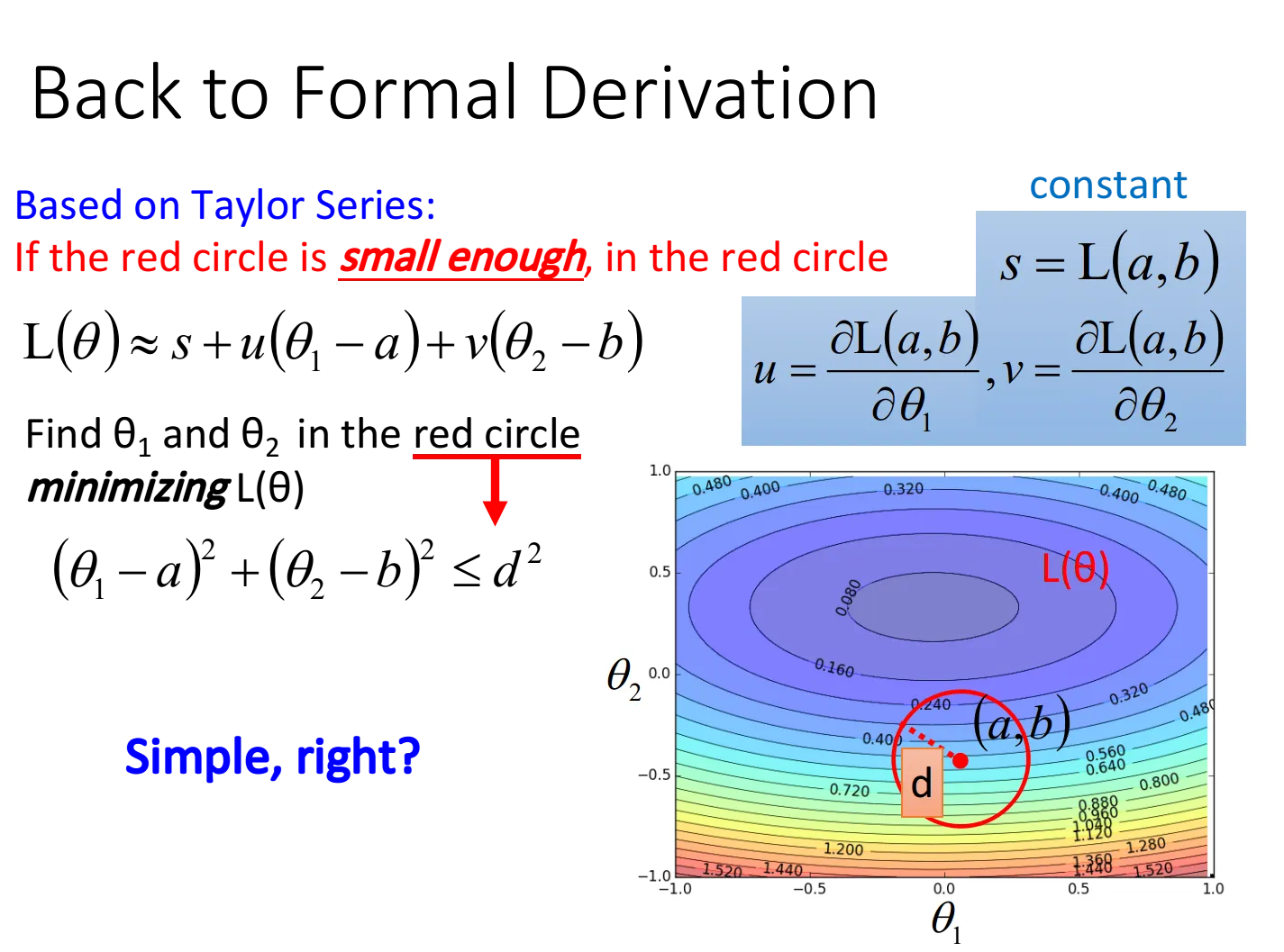
假设用一个限定点的范围，这个圆足够小以满足泰勒展开的精度，那么此时我们的损失函数就可以化简为：

$L(\theta)≈L(a,b)+\frac{\partial L(a,b)}{\partial \theta_1}(\theta_1-a)+\frac{\partial L(a,b)}{\partial \theta_2}(\theta_2-b)$

令$s=L(a,b)$，$u=\frac{\partial L(a,b)}{\partial \theta_1}$，$v=\frac{\partial L(a,b)}{\partial \theta_2}$

则$L(\theta)≈s+u\cdot (\theta_1-a)+v\cdot (\theta_2-b)$

假定red circle的半径为d，则有限制条件：$(\theta_1-a)^2+(\theta_2-b)^2≤d^2$

此时去求$L(\theta)_{min}$，这里有个小技巧，把$L(\theta)$转化为两个向量的乘积：$u\cdot (\theta_1-a)+v\cdot (\theta_2-b)=(u,v)\cdot (\theta_1-a,\theta_2-b)=(u,v)\cdot (\Delta \theta_1,\Delta \theta_2)$

观察图形可知，当向量$(\theta_1-a,\theta_2-b)$与向量$(u,v)$反向，且刚好到达red circle的边缘时(用$\eta$去控制向量的长度)，$L(\theta)$最小

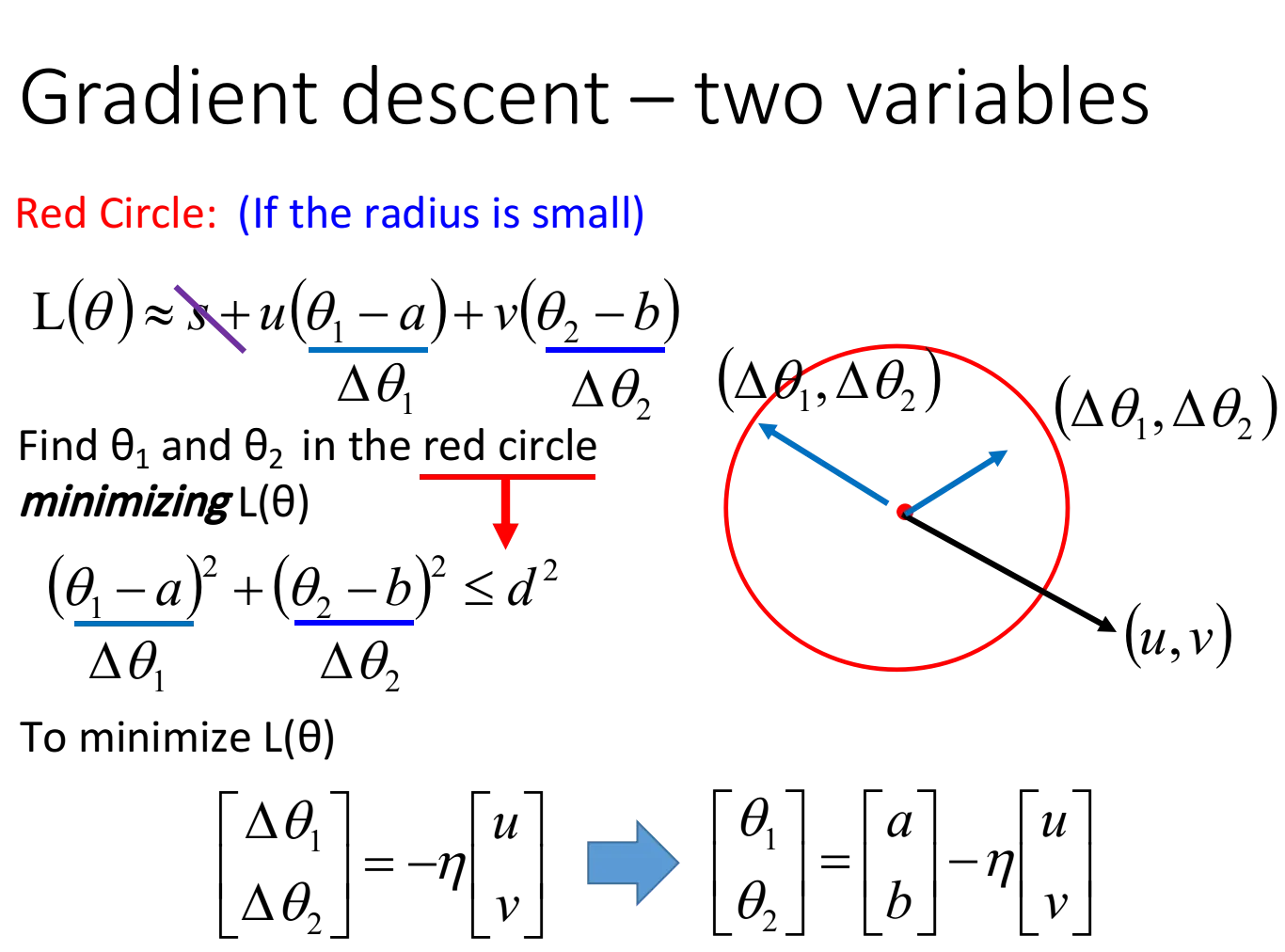
$(\theta_1-a,\theta_2-b)$实际上就是$(\Delta \theta_1,\Delta \theta_2)$，于是$L(\theta)$局部最小值对应的参数为中心点减去gradient的加权 $$ \begin{bmatrix} \Delta \theta_1 \ \Delta \theta_2 \end{bmatrix}= -\eta \begin{bmatrix} u \ v \end{bmatrix}=> \begin{bmatrix} \theta_1 \ \theta_2 \end{bmatrix}= \begin{bmatrix} a\ b \end{bmatrix}-\eta \begin{bmatrix} u\ v \end{bmatrix}= \begin{bmatrix} a\ b \end{bmatrix}-\eta \begin{bmatrix} \frac{\partial L(a,b)}{\partial \theta_1}\ \frac{\partial L(a,b)}{\partial \theta_2} \end{bmatrix} $$ 这就是gradient descent在数学上的推导，注意它的重要前提是，给定的那个红色圈圈的范围要足够小，这样泰勒展开给我们的近似才会更精确，而$\eta$的值是与圆的半径成正比的，因此理论上learning rate要无穷小才能够保证每次gradient descent在update参数之后的loss会越来越小，于是当learning rate没有设置好，泰勒近似不成立，就有可能使gradient descent过程中的loss没有越来越小

当然泰勒展开可以使用二阶、三阶乃至更高阶的展开，但这样会使得运算量大大增加，反而降低了运行效率

梯度下降算法的限制

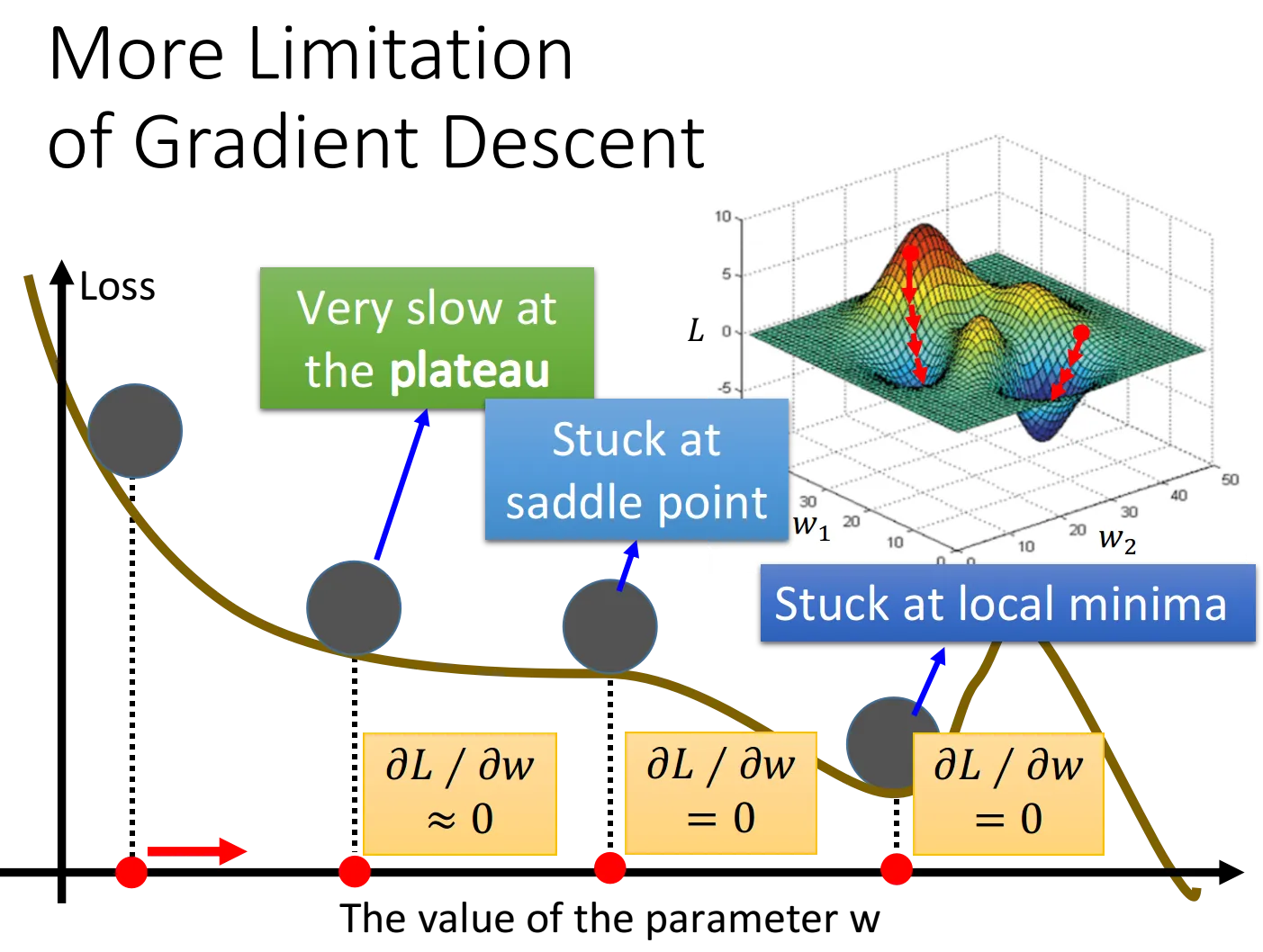
综上，Gradient Descent的限制是，它在Gradient即微分值接近于0的地方就会停下来，而这个地方不一定是global minimum，它可能是local minimum，可能是saddle point鞍点，甚至可能是一个loss很高的plateau平缓高原

Reference:

• An overview of gradient descent optimization algorithms
• Gradient-Descent
• Machine Learning week 1: Cost Function, Gradient Descent and Univariate Linear Regression
• 知乎答案:梯度下降的参数更新公式是如何确定的
• Gradient Descent For Machine Learning
• 线性回归有精确的解析解为什么还要用梯度下降得到数值解？
• 线性回归最小二乘法与梯度下降法数学推导及 Python 实现

以上内容也可以到我的 Github 去查看(附了相应实现代码哟) Machine-Learning-Notes