[读书笔记]《西瓜书》第三章 线性模型 补充

第三章 线性模型 补充

前提假设

引用知乎答案：回归最基本的前提假设是什么？

There are four principal assumptions which justify the use of linear regression models for purposes of inference or prediction:

• linearity and additivity of the relationship between dependent and independent variables:
  • (a) The expected value of dependent variable is a straight-line function of each independent variable, holding the others fixed.
  • (b) The slope of that line does not depend on the values of the other variables.
  • (c) The effects of different independent variables on the expected value of the dependent variable are additive.
• statistical independence of the errors (in particular, no correlation between consecutive errors in the case of time series data)
• homoscedasticity (constant variance) of the errors
  • (a) versus time (in the case of time series data)
  • (b) versus the predictions
  • (c) versus any independent variable
• normality of the error distribution.

个人对上面的翻译：

在使用线性回归模型用来做推断和预测的时候，需要建立在四个假设的基础上是合理的：

• 因变量和自变量之间关系存在线性的关系且具有可加性
  • 当其他自变量不变时，因变量的期望值可以通过任一自变量的一条直线函数得到
  • 该线的斜率不取决于其他因变量的值
  • 不同自变量对因变量期望值的影响是累加的
• 误差的统计独立性（特别是在时间序列数据的情况下，连续错误之间没有相关性）
• 误差之间是的同方差（恒定方差）
  • 与时间之间（对于时间序列数据）
  • 与预测值之间
  • 与任一因变量之间
• 误差是呈现正态分布的

总结一下，即：线性回归是建立在承认数据集存在噪音的基础之上的，而且这些噪声本身是属于同一方差和均值下的正态分布中的样本，换句话说，即假设这些噪声是独立同分布的从一个均值为$\mu$方差为$\sigma$的正态分布中取出的。

最小二乘法（最小平方法）

引用B站大神shuhuai008视频：白板推导系列：线性回归-最小二乘法

这里吐槽一下：我个人觉得最小二乘法这个名称特别难记，还不如最小平方法来的实际

标准定义

最小二乘法，又称最小平方法，是一种数学优化建模方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。 利用最小二乘法可以简便的求得未知的数据，并使得求得的数据与实际数据之间误差的平方和为最小。 “最小二乘法”是对线性方程组，即方程个数比未知数更多的方程组，以回归分析求得近似解的标准方法。

视频中讲解了如何用最小二乘法来进行估计线性回归的闭式解，并且从几何视角和概率视角进行了讲解，相比西瓜书来说要容易理解的多。

样本集的特征构成了一个 $p$ 维的空间，而 $y$ 向量独立于这个空间，目的即为找到一条直线离这个 $y$ 向量最近

这里前者可以看做将原来的总噪声分布在每个样本之上的，后者则可以看做将原来的总噪声分布在每个特征之上

上面就是我看过视频觉得最有启发的两个点

Lasso和Ridge

首先要明确的一个问题是标准线性回归的公式最终求解的公式为 $\boldsymbol{w}=(X^{T}X)^{-1}X^{T}\boldsymbol{y}$ 中可以看出在计算回归系数的时候我们需要计算矩阵 $X^{T}X$ 的逆，但是如果该矩阵是个奇异矩阵，则无法对其进行求解。

那么什么情况下该矩阵会有奇异性呢?

• $X$ 本身存在线性相关关系(多重共线性)，即非满秩矩阵。

  如果数据的特征中存在两个相关的变量，即使并不是完全线性相关，但是也会造成矩阵求逆的时候造成求解不稳定。

• 当数据特征比数据量还要多的时候，这时候矩阵是一个矮胖型的矩阵，也是非满秩的矩阵。

Lasso和Ridge在损失函数

二者的共同目的都是为了将回归系数 $\boldsymbol{w}$ 收缩到一定的区域内，防止模型的过拟合

Lasso

Lasso的主要思想是构造一个一阶惩罚函数，来得到一个防止过拟合的模型。

本质为:

以两个变量为例，标准线性回归的loss function还是可以用二维平面的等值线表示，Lasso的约束条件可以用方形表示，如下图:

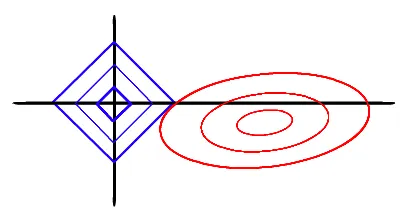
当方形的顶点与抛物面相交时，其切点在坐标轴上的概率更大，因此其对应的权重变为0

其本身特点有：

• Lasso 对于异常值不敏感
• Lasso 可以将权重较小的值，置为0，因此可以用作特征选择
• Lasso 可能存在多个最优解

Ridge

Ridge的主要思想是构造一个二阶惩罚函数，来得到一个防止过拟合的模型。

本质为:

以两个变量为例, 标准线性回归的loss function还是可以用二维平面的等值线表示。而Ridge限制条件相当于在二维平面的一个圆。如下图：

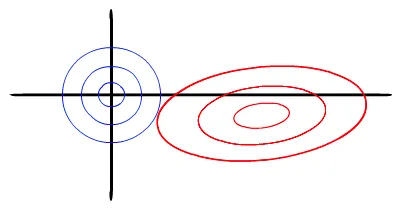
这个时候等值线与圆相切的点便是在约束条件下的最优点，但通常情况下，其切点在坐标轴上的概率较小，因此其对应的权重很难变为0

其本身的特点有：

• Ridge 在计算过程中十分方便
• Ridge 一定只有一条最好的预测线
• Ridge 对于异常值要比 Lasso 敏感一点

对比

这里详细的内容参见 知乎答案 L1正则与L2正则的特点是什么，各有什么优势？

这里摘抄两个图粘贴在此，以作为方便记忆上面的Lasso和Ridge各自的特点

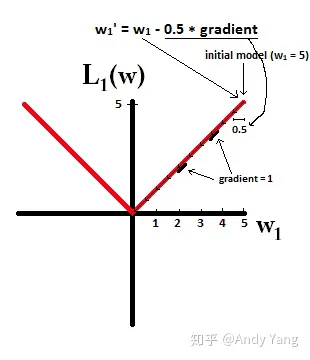
在梯度更新时，不管 L1 的大小是多少（只要不是0）梯度都是1或者-1，所以每次更新时，它都是稳步向0前进。

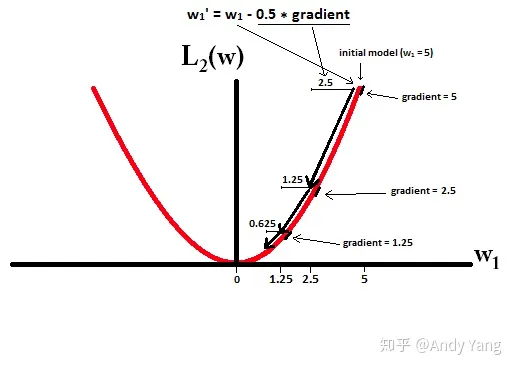
而看 L2 的话，就会发现它的梯度会越靠近0，就变得越小。

也就是说加了 L1 正则的话基本上经过一定步数后很可能变为0，而 L2 几乎不可能，因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。

以上内容也可以到我的 Github 去查看(附了相应实现代码哟) Machine-Learning-Notes