[读书笔记]《西瓜书》第二章 模型评估与选择

第二章 模型评估与选择

---

2.1 经验误差与过拟合

基本概念

错误率（error rate）

把分类错误的样本数占样本总数的比例

• $E=a/m$

精度（accuracy）

精度 = 1 - 错误率

• $E=1-a/m$

误差（error）

均指误差期望

• 把学习器的实际预测输出与样本的真实输出之间的差异称为误差
• 学习器在训练集上的误差称为 “训练误差”（training error）或 “经验误差”（empirical error）
• 在新样本上的误差称为 “泛化误差”（generalization error）

机器学习的目标：得到泛化误差小的学习器

机器学习的关键障碍，无法彻底避免，只能“缓解”

补充：(因为这是一个 P = NP 问题：P就是能在多项式时间内解决的问题，NP就是能在多项式时间验证答案正确与否的问题)

过拟合（overfitting）

• 把训练样本自身的一些特点当作了潜在样本都会有的一般性质
• 又称 “过配”

欠拟合（underfitting）

• 指对训练样本的一般性质尚未学好
• 又称 “欠配”

衡量学习能力是否 “强大”：学习算法 和 数据内涵

模型选择（model selection）问题

2.2 评估方法

实验测试

测试集（testing set）

• 从样本真实分布中独立同分布采样的
• 测试机与训练集尽可能互斥

测试误差（testing error）$\approx$ 泛化误差

分层采样（stratified sampling）

留出法（hold-out）

直接将数据集划分为两个互斥的集合

测试集较小时，评估结果的方差较大；训练集小时，评估结果的偏差较大

常见做法 2/3 ~ 4/5 的样本作为训练集，剩余样本用于测试

交叉验证法（cross validation）

将数据集划分为k个大小相似的互斥子集

每个子集都应该尽可能保持数据分布的一致性，即从D中分层采样得到

每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集

• 拥有k组的训练和测试集
• 可进行k次训练和测试
• 最终结果为k次结果取均值

与留出法相似，每次划分会影响结果，因此需要使用不同的划分重复 p 次，即 p 次 k 折交叉验证 == p * k 次留出法

当k和数据集数量一致时，称之为留一法（Leave One Out）简称：LOO

• 相当准确，不受划分影响
• 模型计算开销大

自助采样（bootstrap sampling）

自助法（bootstrapping）

自助采样过程

$Step1$: 对包含m个样本的数据集$D$，进行采样产生数据集$D'$

$Step2$:每次随机从$D$中挑选一个样本，将其拷贝放入$D'$中

$Step3$:步骤二重复$m$次，得到包含$m$个样本的数据集$D'$，就是最终结果

自助采样的特点

$D'$ 中会有一部分重复样本

样本在$m$次采样中始终不被采到的概率是$(1-\frac{1}{m})^m$

$\lim_{m\to\infty}(1-\frac{1}{m})^m = \frac{1}{e}\approx 0.368$

通过自助采样，初始数据集中约有36.8%的样本未出现在采样数据集中

$D'$用作训练集，$D \backslash D'$作为测试集 ($\backslash$ 代表集合减法)

• 实际评估的模型和期望评估的模型都有使用m个训练样本
• 越有 1/3 的数据没有出现在训练集中，用于测试

测试结果，称为 “包外估计” （out of bag estimate）

调参与最终模型

调参（parameter tuning）

参数类型

• 超参数: 算法本身的参数, 数目常在10个以内, 人工设定多个参数候选值后产生模型

• 参数: 模型的参数, 数目可能很多, 通过学习来产生多个候选模型

理想状态是对每种取值都做模型训练

对每一个参数选定一个选参范围和变化步长

最终模型

$Step1$: 将包含$m$个样本的数据集$D$，拆分成训练数据和测试数据

$Step2$: 对训练数据拆分成训练集和验证集

$Step3$: 使用训练集训练模型，借助验证集调整超参数，选定模型

$Step4$: 通过测试集对模型进行最终的评估

$Step5$: 最终使用全部$m$个样本按选定的算法和参数设置训练模型

2.3 性能度量

定义

对学习器的泛化性能进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量（performance measure）

均方误差（mean squared error）

回归任务最常用

给定样例集$D=\left\{(\boldsymbol{x_1}, y_1),(\boldsymbol{x_2}, y_2),…,(\boldsymbol{x_m}, y_m)\right\}$，其中$y_i$是示例$\boldsymbol{x_i}$的真实标记

$E(f;D)=\frac{1}{m}\sum_{i=1}^m(f(\boldsymbol{x_i})-y_i)^2$

$E(f;D)=\int_{\boldsymbol{x}\sim D}(f(\boldsymbol{x})-y)^2p(\boldsymbol{x})d\boldsymbol{x}$

错误率和精度

错误率（error rate）

分类错误的样本数占样本总数的比例

• $E(f;D)=\frac{1}{m}\sum_{i=1}^m\mathbb{I}(f(\boldsymbol{x_i})\neq y_i)$
• $E(f;D)=\int_{\boldsymbol{x}\sim D}\mathbb{I}(f(\boldsymbol{x})\neq y)p(\boldsymbol{x})d\boldsymbol{x}$

精度（accuracy）

分类正确的样本数占样本总数的比例

• $acc(f;D) = \frac{1}{m}\sum_{i=1}^m\mathbb{I}(f(\boldsymbol{x_i})= y_i)$
• $E(f;D)=\int_{\boldsymbol{x}\sim D}\mathbb{I}(f(\boldsymbol{x})= y)p(\boldsymbol{x})d\boldsymbol{x}$

查全率 & 查准率 & F1

分类混淆矩阵

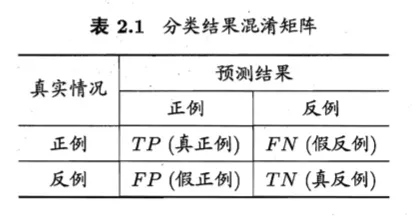
纵向是预测，横向是真实

纵向排在真实后

• 真正例（true positive）TP
• 假正例（false positive）FP
• 真反例（true negative）TN
• 假反例（false negative）FN

查准率 P（precision）& 准确率

• “挑出的西瓜中有多少是好瓜”
• $P = \frac {TP} {TP+FP}$

查全率 R（recall）& 召回率

• “所有好瓜中有多少的比例被挑了出来”
• $R = \frac {TP} {TP + FN}$

P-R 曲线

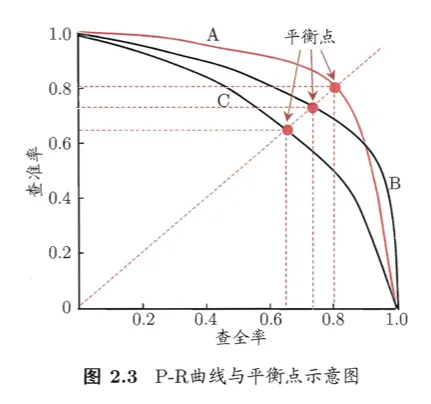
以查准率为纵轴，查全率为横轴作图

如何利用P-R曲线判定两个学习器的性能?

比较曲线下的面积的大小

• “平衡点”（Break-Even Point）BEP
• “查准率=查全率”时的取值

$F1$ 度量

• $F1=\frac{2 \times P \times R}{P + R}=\frac{2\times TP}{m+TP-TN}$
• 源于查准率与查全率的调和平均（harmonic mean）
  • $\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$

$F_{\beta}$ 度量

• $F 1=\frac{(1+\beta^2) \times P \times R}{(\beta^2 \times P) + R}$
• 源于查准率与查全率的加权调和平均
  • $\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})$
• $\beta$ 度量了查全率和查准率的相对重要性
  • $\beta=1$退化为标准型$F1$值
  • $\beta>1$时查全率有更大影响
  • $\beta<1$时查准率有更大影响

n次二分类实现的多分类问题

• 先分别计算，再求平均值

  • 宏查准率: macro-P = $\frac{1}{n}\sum_{i=1}^{n}P_{i}$
  • 宏查全率: macro-R = $\frac{1}{n}\sum_{i=1}^{n}R_{i}$
  • 宏F1: macro-F1 = $\frac{2 \times \text{macro-P} \times \text{macro-R}}{\text{macro-P + macro-R}}$

• 先求平均值，再分别计算

  • 平均值分别记为：$\overline{TP}、\overline{FP}、\overline{TN}、\overline{FN}$
  • 微查准率: $\text{micro-P}=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}$
  • 微查全率: $\text{micro-R}=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}$
  • 微F1: $\text{micro-F1}=\frac{2 \times \text{micro-P} \times \text{micro-R}}{\text{micro-P}+\text{micro-R}}$

ROC与AUC

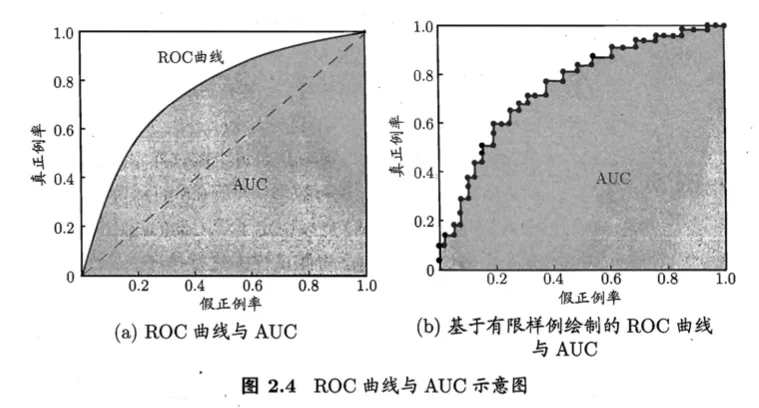
纵轴是“真正例率”（True Positive Rate，简称TPR），横轴是“假正例率”（False Positive Rate，简称FPR）

ROC（Receiver Operating Characteristic）

“受试者工作特征”曲线

• $TPR=\frac{TP}{TP+FN}$
• $FPR=\frac{FP}{TN+FP}$

AUC（Area Under ROC Curve）

ROC曲线下的面积

$AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1})$

AUC是考虑样本预测的排序质量，因此它与排序误差有紧密联系

排序导致的损失公式

考虑每一个正反例，如果预测值小于反例，记1，若相等，记0.5

$AUC = 1 - \ell_{rank}$

代价敏感错误率与代价曲线

非均等代价（unequal cost）

为权衡不同类型错误所造成的不同损失

代价矩阵（cost matrix）

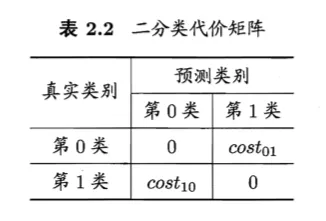
• $cost_{ij}$表示将第i类样本预测为第j类样本的代价
• 一般来说，$cost_{ij}=0$
• 若将第0类判别为第1类所造成的损失更大，则$cost_{01} > cost_{10}$
• 损失程度相差越大，$cost_{01}$与$cost_{10}$值的差别越大

在非均等代价下，我们所希望的不再是简单地最小化错误次数，而是希望最小化“总体代价”（total cost）

代价敏感（cost-sensitive）错误率公式:

$E(f;D;cost)=\frac{1}{m}(\sum_{\boldsymbol{x_i} \in D^+}\mathbb{I}(f(\boldsymbol{x_i}) \neq y_i) \times cost_{01} + \sum_{\boldsymbol{x_i} \in D^-}\mathbb{I}(f(\boldsymbol{x_i}) \neq y_i) \times cost_{10})$

代价曲线（cost curve）

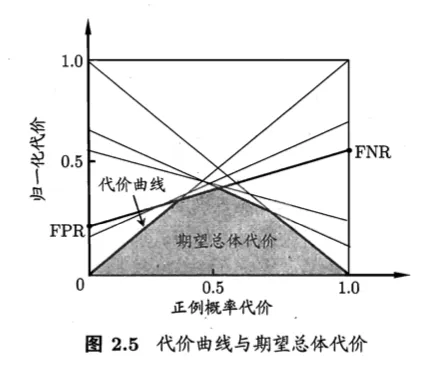
$p=\frac{m^+}{m};m是样例数，m^+是正样例数$

横轴

• 取值为 [0, 1] 的正例概率代价
• $P(+)cost=\frac{p \times cost_{01}}{p \times cost_{01} + (1 - p) \times cost_{10}}$

纵轴

• 取值为 [0, 1] 的归一化代价
• $cost_{norm}=\frac{FNR \times p \times cost_{01} + FPR \times (1-p) \times cost_{10}}{p \times cost_{01} + (1-p) \times cost_{10}}$

当判断阈值threshold一定时，就确定了一组相应的混淆矩阵，而根据样例中的正样例数量的比率的不同，产生了不同的代价期望

在非均等代价下，ROC曲线不能直接反映出学习器的期望总体代价

目的：根据正例在样本中的比值的不同，找到使得代价总期望最小的模型的阈值

2.4 比较检验

问题

1、测试集上的性能与真实的泛化性能未必相同

2、测试集的不同反映出来的性能不同

3、机器学习算法本身有一定的随机性，同一测试集上的性能也不同

测试错误率与泛化错误率未必相同，但二者理论上相近

真实情况下：

泛化错误率为 $\epsilon$ 的学习器在一个样本上犯错的概率是 $\epsilon$

统计情况下：

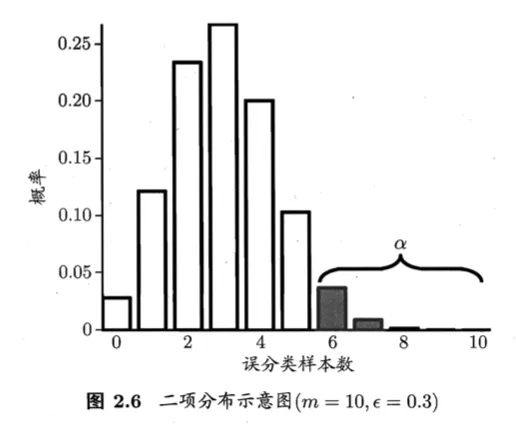
测试错误率 $\hat\epsilon$ 意味着在 $m$ 个测试样本中恰有 $\hat\epsilon \times m$ 个被误分类

统计假设检验（hypothesis test）

若在测试集上观察到学习器A比学习器B好，则A的泛化性能是否在统计意义上优于B，以及这个结论的把握有多大

参考知乎答案

符号

• $\epsilon$ - 泛化错误率

  是学习器的内在属性，是客观存在的值，但是无法观测

• $\epsilon_{0}$ - 泛化错误率

  是人为设定的一个值，用于推测真实的泛化错误率

  • $\epsilon = \epsilon_{0}$
  • $\epsilon \le \epsilon_{0}$
  • $\epsilon \ge \epsilon_{0}$
• $\hat {\epsilon}$ - 测试错误率

  是经过实验观测到的测试错误率，跟泛化错误率存在某种关系

• $\overline{\epsilon}$ - 检验临界值

  是测试错误率的上限，为了使得假设条件得到满足的最大测试错误率的值

理念

假设测试样本是从样本总体分布中独立采样而得，且学习器的泛化错误率为$\epsilon$

在$m$个样本中，有$m'$个样本被误分类，其余样本全部正确分类的概率是:

$$\begin{pmatrix} m \\ m' \end{pmatrix}\epsilon^{m'}(1-\epsilon)^{m-m'}$$

由此可估算出其恰将$\hat \epsilon \times m$ 个样本误分类的概率是：

$$P(\hat{\epsilon};\epsilon)=\begin{pmatrix} m \\ \hat{\epsilon} \times m \end{pmatrix}\epsilon^{\hat{\epsilon} \times m}(1-\epsilon)^{m-\hat{\epsilon}\times m}$$

常用方法

t - 检验（t-test)

存在k个测试错误率，$\hat{\epsilon_{1}}，\hat{\epsilon_{2}}，…，\hat{\epsilon_{k}}$

• 平均测试错误率: $\mu = \frac {1} {k} \sum_{i=1}^k \hat{\epsilon_{i}}$
• 方差: $\sigma^2=\frac{1}{k-1}\sum_{i=1}^k(\hat{\epsilon_{i}}-\mu)^2$

$k$个测试错误率可以看作泛化错误率 $\epsilon$ 的独立采样 即：

• 服从自由度为 $k-1$ 的 t-分布
• $\tau_{t}=\frac{\sqrt{k}(\mu-\epsilon_{0})}{\sigma}$

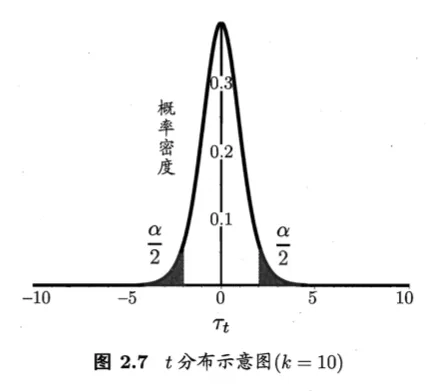
用于根据小样本来估计呈正态分布且方差未知的总体的均值 自由度越小，曲线越平坦，自由度越大，越接近标准正态分布 其本质是一族曲线，每一个自由度的值都可以确定其中唯一一条曲线

• 双边检验的临界值: $t_{\frac{\alpha}{2},k-1}$

• 结论

• 当 $\tau_{t} \le t_{\frac{\alpha}{2},k-1}$ 则假设不能被拒绝，即认为两个学习器的性能没有显著差别

• 当 $\tau_{t} > t_{\frac{\alpha}{2},k-1}$ 则假设被拒绝，且平均错误率较小的那个学习器性能更优

交叉验证 t 检验

若两个学习期的性能相同，则它们使用相同的训练集和测试集得到的测试错误率应相同，即：$\epsilon_{i}^A = \epsilon_{i}^B$

k折交叉验证法

步骤

• $Step1:$分别得到一组成对测试错误率$\epsilon_{1}^A，\epsilon_{2}^B，……，\epsilon_{k}^A$和$\epsilon_{1}^B，\epsilon_{2}^B，……，\epsilon_{k}^B$
• $Step2:$对每对结果求查：$\Delta_{i}=\epsilon_{i}^A-\epsilon_{i}^B$，形成一组差值集合 $\Delta_{1}、\Delta_{2}、……、\Delta_{k}$
• $Step3:$使用Step2中的差值集合来对“学习器A与学习器B性能相同”这个假设做t-检验
• $Step4:$计算出差值的均值 $\mu$ 和 方差 $\sigma^2$，在显著度 $\alpha$ 下，计算变量 $$\tau_t =|\frac{\sqrt{k}\mu}{\sigma}|$$

5x2交叉验证法 (5次2折交叉验证)

为了缓解k折交叉验证法过高估计假设成立提出的解决方案

步骤

• $Step1:$在每次进行2折交叉验证之前随机将数据打乱，使得五次交叉验证中的数据划分不重复
• $Step2:$对两个学习器A和B，第i次2折交叉验证将产生两对测试错误率，分别对其求差 $$\Delta_{i}^{1} = \epsilon_{i}^{A_1}-\epsilon_{i}^{B_1}，\Delta_{i}^{2} = \epsilon_{i}^{A_2}-\epsilon_{i}^{B_2}$$
• $Step3:$为了缓解测试错误率的非独立性，仅计算第1次2折交叉验证的结果平均值 $\mu = \frac{(\Delta_1^1+\Delta_1^2)}{2}$，但对每次2折实验的结果都计算出其方差 $$\sigma^2=(\Delta_i^1-\frac{\Delta_i^1+\Delta_i^2}{2})^2+(\Delta_i^2-\frac{\Delta_i^1+\Delta_i^2}{2})^2$$
• $Step4:$计算变量 $$\tau_t = \frac{\mu}{\sqrt{\frac{\sum_{i=1}^5\sigma_{i}^2}{5}}}$$

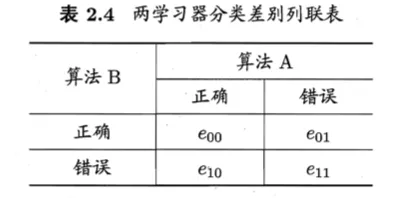
McNemar 检验

• 列联表（contingency table）

  • 通常情况下，变量 $|e_{01}-e_{10}|$ 应当服从正态分布
  • 特殊情况下，如果两个学习器性能相同，那么 $e_{01} = e_{10}$

• 计算变量 $$\tau_{\chi^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01} - e_{10}}$$

  • 服从自由度为1的卡方分布，即标准正态分布变量的平方
  • 如果通过卡方分布进行评估，则通过将上表的$e_{01}$与$e_{10}$两个频率中较小的一个加上0.5、较大的一个减去0.5来进行连续性校正。这种纠正在统一降低差异的绝对值$e_{01}-e_{10}$中具有明显的效果。提出后为式子 -1
  • 最终结论看平均错误率较小的学习器性能更优

Friedman 检验

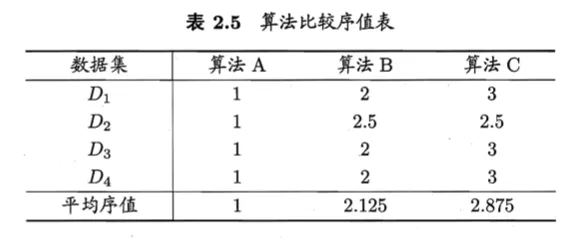
步骤

• $Step1:$假设四个数据集 $D_{1}，D_{2}，D_{3}，D_{4}$，分别对A、B、C算法进行测试
• $Step2:$在每个数据集上对测试性能好坏进行排序，并赋予序值，如果相同，则平均序值
• $Step3:$对每一个算法在不同数据集上的序值进行求平均，得到平均序值
• $Step4:$然后使用Friedman检验判断这些算法性能是否相同

Nemenyi 后续检验（Nemenyi post-hoc test）

• 计算平均序值差别的临界值域
• $CD=q_{\alpha}\sqrt{\frac{k(k+1)}{6N}}$

  $q_{\alpha}$是Tukey分布的临界值

• 若两个算分的平均序值之差超过了临界值域，则以相应的置信度拒绝“两个算法性能相同”这一假设

Friedman 检验图

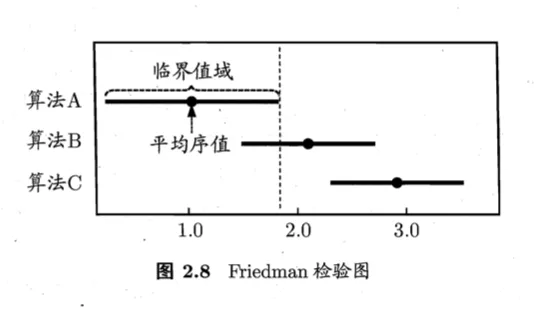
• 纵轴是各个算法，横轴是平均序值
• 每个算法以原点显示其平均序值，然后线段的长度描述临界值域的大小
• 若线段重叠，则说明算法之间没有显著性能差别，否则即说有显著性能差别

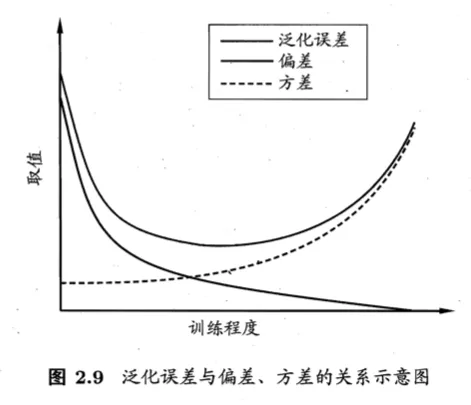
2.5 偏差与方差

“偏差-方差分解”（bias-variance decomposition）用来解释其学习器为什么具备这样的性能

对于测试样本$\boldsymbol{x}$

符号说明

• $y$ 为样本的真实标记
• $y_{D}$ 为样本在数据集中的标记
• $f(\boldsymbol{x};D)$ 为学习器输出的样本标记

偏差-方差分解公式

$E(f;D)=bias^2(\boldsymbol{x})+var(\boldsymbol{x})+\varepsilon^2$

• 学习算法的期望预测: $$\overline{f}(\boldsymbol{x})=\mathbb{E}_{D}[f(\boldsymbol{x};D)]$$
• 使用样本数相同的不同训练集产生的方差: $$var(\boldsymbol{x})=\mathbb{E}_{D}[(f(\boldsymbol{x};D)-\overline{f}(\boldsymbol{x}))^2]$$
• 噪声: $$\varepsilon^2=\mathbb{E}_D[(y_D-y)^2]$$
• 偏差: $$bias^2(\boldsymbol{x})=(\overline{f}(\boldsymbol{x})-y)^2$$

结论

• 偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力
• 方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
• 噪声：表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度

泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的

• 使得偏差较小，即能充分拟合数据
• 使得方差较小，即使得数据扰动产生的影响小

---

以上内容也可以到我的 Github 去查看(附了相应实现代码哟) Machine-Learning-Notes

笔记内容（XMind、Markdown、PNG）

第二章 模型评估与选择.png (5917 kb)

第二章 模型评估与选择.xmind (2879 kb)